圖(graph)是由節點(node)和邊(edge)組合而成的非線性結構,如果我們想要從其中的一個節點開始,走訪到其有直接或是間接連接的其它所有節點,可以依靠深度優先搜尋法(DFS, Depth-first Search)或是廣度優先搜尋法(BFS, Breadth-first Search)來達成。
檔案系統的結構其實就是樹狀(tree)結構,而樹屬於圖的一種,所以檔案系統也適用於深度優先搜尋和廣度優先搜尋。就拿檔案搜尋來說明深度優先搜尋和廣度優先搜尋有什麼不同吧!
我們都知道,檔案可以細分為:有子檔案的「目錄」和沒有子檔案的「檔案」。假設有個目錄的檔案結構是以下這個樣子:
pictures
├── animals
├── a1.jpg
└── a2.jpg
└── plants
├── p1.jpg
└── p2.jpg
試想一下,當我們想要用檔案瀏覽器查看一個pictures目錄底下,包含其子目錄下的所有檔案時,會是怎麼樣的情形。
如果是使用深度優先搜尋法的話,只要看到目錄就會立刻點入。所以我們在點入pictures目錄後,接著看到animals目錄,基於深度優先搜尋法的原則,我們會立刻點入animals目錄。再來我們就會看到a1.jpg和a2.jpg檔案。然後回到上一頁,也就是pictures目錄後,看到animals目錄之後的plants目錄,我們繼續點入,就會看到p1.jpg和p2.jpg檔案。
而如果是使用廣度優先搜尋法的話,必須要看完一層目錄後,才會再看下一層。所以我們在點入pictures目錄後,雖然首先會看到animals目錄,但基於廣度優先搜尋法的原則,我們還要先繼續看pictures目錄中的其它檔案,所以接下來會再看到pictures目錄中還有plants目錄。再來就是點入animals目錄,就會看到其中有a1.jpg和a2.jpg檔案。然後回到上一頁,也就是pictures目錄後,點入plants目錄,就會看到其中有p1.jpg和p2.jpg檔案。
深度優先搜尋法和廣度優先搜尋法隨著應用方式的不同,程式實作方式也會有很大的差異,不過概念就像是以上這樣。
樹的深度優先搜尋和廣度優先搜尋
樹的深度優先搜尋和廣度優先搜尋之過程
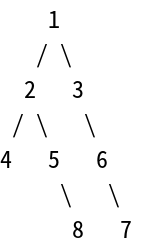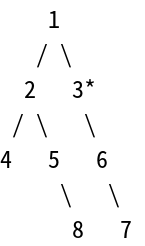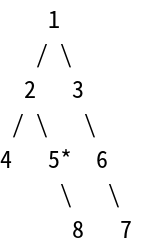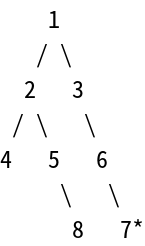
假設現在有個樹狀資料,內容如下:
1
/ \
2 3
/ \ \
4 5 6
\ \
8 7
我們想要在這個樹中找出數值6。以下將分別探討其在深度優先搜尋和廣度優先搜尋時的過程。
深度優先搜尋
首先從樹根也就是數值1的位置開始。
1*
/ \
2 3
/ \ \
4 5 6
\ \
8 7
因為數值1不等於數值6,所以再從數值1這個節點的底下節點來找。
然後看到數值2的這個節點。
1
/ \
2* 3
/ \ \
4 5 6
\ \
8 7
因為數值2不等於數值6,然後又要深度優先的關係,所以再從數值2這個節點的底下節點來找。
然後看到數值4的這個節點。
1
/ \
2 3
/ \ \
4* 5 6
\ \
8 7
因為數值4不等於數值6,然後又要深度優先的關係,所以再從數值4這個節點的底下節點來找。
但是數值4這個節點底下已經沒有子節點了,所以會跳去看數值5這個節點。
1
/ \
2 3
/ \ \
4 5* 6
\ \
8 7
因為數值5不等於數值6,然後又要深度優先的關係,所以再從數值5這個節點的底下節點來找。
然後看到數值8的這個節點。
1
/ \
2 3
/ \ \
4 5 6
\ \
8* 7
因為數值8不等於數值6,然後又要深度優先的關係,所以再從數值8這個節點的底下節點來找。
但是數值8這個節點底下已經沒有子節點了,且數值5和數值2也都沒有其它還沒看過的節點,所以會跳去看數值3這個節點。
1
/ \
2 3*
/ \ \
4 5 6
\ \
8 7
因為數值3不等於數值6,然後又要深度優先的關係,所以再從數值3這個節點的底下節點來找。
然後看到數值6的這個節點。
1
/ \
2 3
/ \ \
4 5 6*
\ \
8 7
數值6正是我們要找的節點!
下面這個動畫演示了整棵樹使用深度搜尋來走訪所有節點過程:
廣度優先搜尋
首先從樹根也就是數值1的位置開始。
1*
/ \
2 3
/ \ \
4 5 6
\ \
8 7
因為數值1不等於數值6,所以再從數值1這個節點的底下節點來找。
然後看到數值2的這個節點。
1
/ \
2* 3
/ \ \
4 5 6
\ \
8 7
因為數值2不等於數值6,然後又要廣度優先的關係,所以再繼續從數值1這個節點的底下節點來找。
然後看到數值3的這個節點。
1
/ \
2 3*
/ \ \
4 5 6
\ \
8 7
因為數值3不等於數值6,然後又要廣度優先的關係,所以再繼續從數值1這個節點的底下節點來找。
但是數值1這個節點的子節點都已經被看過了,所以會跳去看數值2這個節點底下的子節點。
然後就會看到數值4的這個節點。
1
/ \
2 3
/ \ \
4* 5 6
\ \
8 7
因為數值4不等於數值6,然後又要廣度優先的關係,所以再繼續從數值2這個節點的底下節點來找。
然後看到數值5的這個節點。
1
/ \
2 3
/ \ \
4 5* 6
\ \
8 7
因為數值5不等於數值6,然後又要廣度優先的關係,所以再繼續從數值2這個節點的底下節點來找。
但是數值2這個節點的子節點都已經被看過了,所以會跳去看數值3這個節點底下的子節點。
然後就會看到數值6的這個節點。
1
/ \
2 3
/ \ \
4 5 6*
\ \
8 7
數值6正是我們要找的節點!
下面這個動畫演示了整棵樹使用廣度搜尋來走訪所有節點過程:
樹的深度優先搜尋和廣度優先搜尋之實作
use std::{cell::RefCell, collections::LinkedList, rc::Rc};
#[derive(Debug)]
pub struct Node {
pub value: i32,
pub children: Vec<Rc<RefCell<Node>>>,
}
impl Node {
pub fn new(value: i32) -> Self {
Node {
value,
children: Vec::new(),
}
}
fn rc_equal(a: &Rc<RefCell<Node>>, b: &Rc<RefCell<Node>>) -> bool {
let ref_a = a.borrow();
let ref_b = b.borrow();
std::ptr::eq(&*ref_a, &*ref_b)
}
pub fn is_child(&self, node: &Rc<RefCell<Node>>) -> bool {
for child in self.children.iter() {
if Self::rc_equal(node, child) {
return true;
}
}
false
}
pub fn add_adjacent_node(node: Rc<RefCell<Node>>, child: Rc<RefCell<Node>>) {
let mut borrowed_node = node.borrow_mut();
if !borrowed_node.is_child(&child) {
borrowed_node.children.push(child.clone());
}
}
}
pub fn dfs_recursively(node: Rc<RefCell<Node>>, target_value: i32) -> Option<Rc<RefCell<Node>>> {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
for child in ref_node.children.iter() {
if let Some(node) = dfs_recursively(child.clone(), target_value) {
return Some(node);
}
}
None
}
pub fn dfs(node: Rc<RefCell<Node>>, target_value: i32) -> Option<Rc<RefCell<Node>>> {
let mut stack = Vec::new();
stack.push(node);
while let Some(node) = stack.pop() {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
for child in ref_node.children.iter().rev() {
stack.push(child.clone())
}
}
None
}
pub fn bfs(node: Rc<RefCell<Node>>, target_value: i32) -> Option<Rc<RefCell<Node>>> {
let mut queue = LinkedList::new();
queue.push_back(node);
while let Some(node) = queue.pop_front() {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
for child in ref_node.children.iter() {
queue.push_back(child.clone())
}
}
None
}
pub fn bfs_2_stacks(node: Rc<RefCell<Node>>, target_value: i32) -> Option<Rc<RefCell<Node>>> {
let mut stack_1 = Vec::new();
let mut stack_2 = Vec::new();
stack_1.push(node);
loop {
while let Some(node) = stack_1.pop() {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
for child in ref_node.children.iter() {
stack_2.push(child.clone())
}
}
while let Some(node) = stack_2.pop() {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
for child in ref_node.children.iter() {
stack_1.push(child.clone())
}
}
if stack_1.is_empty() {
break;
}
}
None
}
樹的深度優先搜尋和廣度優先搜尋之複雜度
以#{{v}}#來表示節點的數量。以#{{e}}#來表示邊的數量。
| 項目 |
值 |
備註 |
| 最差時間複雜度 |
#{{O(v + e)}}# |
|
| 最佳時間複雜度 |
#{{O(1)}}# |
第一個走訪到的節點就是我們想找的節點。 |
| 平均時間複雜度 |
#{{O(v + e)}}# |
|
| 最差空間複雜度 |
#{{O(v)}}# |
|
圖的深度優先搜尋和廣度優先搜尋
圖的深度優先搜尋和廣度優先搜尋的方式和樹的差不多,但圖的邊可以是雙向的,而且同一個節點可能會有許多個進入邊(in-edge),所以圖在使用深度優先搜尋和廣度優先搜尋時,要另外去記錄哪些節點已經走訪過了,避免重複走訪。
記錄已走訪的節點的方式有兩種。第一種就是直接替節點多加一個欄位,用來儲存這個節點是否已經走訪過,不過這個會有一些重用時要重設的問題。第二種是在搜尋的時候,另外用一個結構去儲存已經走訪過的節點,不過這個方式可能會增加時間複雜度或是空間複雜度。
這篇文章將會選擇使用第二種方式來實作圖的深度優先搜尋和廣度優先搜尋演算法。
圖的深度優先搜尋和廣度優先搜尋之實作
use std::{
cell::RefCell,
collections::{HashSet, LinkedList},
rc::Rc,
};
#[derive(Debug)]
pub struct Node {
pub value: i32,
pub reachable_nodes: Vec<Rc<RefCell<Node>>>,
}
impl Node {
pub fn new(value: i32) -> Self {
Node {
value,
reachable_nodes: Vec::new(),
}
}
fn rc_equal(a: &Rc<RefCell<Node>>, b: &Rc<RefCell<Node>>) -> bool {
let ref_a = a.borrow();
let ref_b = b.borrow();
std::ptr::eq(&*ref_a, &*ref_b)
}
pub fn is_reachable_node(&self, node: &Rc<RefCell<Node>>) -> bool {
for reachable_node in self.reachable_nodes.iter() {
if Self::rc_equal(node, reachable_node) {
return true;
}
}
false
}
pub fn add_adjacent_node(node: Rc<RefCell<Node>>, reachable_node: Rc<RefCell<Node>>) {
{
let mut borrowed_node = node.borrow_mut();
if !borrowed_node.is_reachable_node(&reachable_node) {
borrowed_node.reachable_nodes.push(reachable_node.clone());
}
}
{
let mut borrowed_reachable_node = reachable_node.borrow_mut();
if !borrowed_reachable_node.is_reachable_node(&node) {
borrowed_reachable_node.reachable_nodes.push(node);
}
}
}
pub fn drop_graph(node: Rc<RefCell<Node>>) {
let mut stack = Vec::new();
stack.push(node);
while let Some(node) = stack.pop() {
let mut ref_node = node.borrow_mut();
for reachable_node in ref_node.reachable_nodes.iter().rev() {
stack.push(reachable_node.clone())
}
ref_node.reachable_nodes.clear();
}
}
}
pub fn dfs(node: Rc<RefCell<Node>>, target_value: i32) -> Option<Rc<RefCell<Node>>> {
let mut visited: HashSet<*const Node> = HashSet::new();
let mut stack = Vec::new();
stack.push(node);
while let Some(node) = stack.pop() {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
visited.insert(&*ref_node as *const Node);
'outer: for reachable_node in ref_node.reachable_nodes.iter().rev() {
if visited.contains(&(&*(reachable_node.borrow()) as *const Node)) {
continue 'outer;
}
stack.push(reachable_node.clone())
}
}
None
}
pub fn bfs(node: Rc<RefCell<Node>>, target_value: i32) -> Option<Rc<RefCell<Node>>> {
let mut visited: HashSet<*const Node> = HashSet::new();
let mut queue = LinkedList::new();
queue.push_back(node);
while let Some(node) = queue.pop_front() {
let ref_node = node.borrow();
if ref_node.value == target_value {
return Some(node.clone());
}
visited.insert(&*ref_node as *const Node);
'outer: for reachable_node in ref_node.reachable_nodes.iter() {
if visited.contains(&(&*(reachable_node.borrow()) as *const Node)) {
continue 'outer;
}
queue.push_back(reachable_node.clone())
}
}
None
}
使用額外的HashSet結構來儲存已經走訪過的節點的指標,可以讓空間複雜度和時間複雜度不會顯著增加。



