指數搜尋(Exponential Search)演算法又稱為雙倍搜尋(Doubling Search)演算法或是蔓延搜尋(Galloping Search)演算法,是二元搜尋(Binary Search)演算法的變體。這套演算法可以在已排序好的序列中進行高效率的搜尋,要搜尋的元素在序列中愈前面的話,搜尋效能愈好。
指數搜尋法(Exponential Search)
指數搜尋法的概念
指數搜尋法是基於二元搜尋法的演算法,如果您還不了解二元搜尋法的話,請先參考這篇文章:
指數搜尋法與二元搜尋法的差異在於,它在一開始的時候,並不是直接去選擇序列中間的元素來比較,而是先去比較索引值為20 = 1的元素。如果發現要查找的元素比索引值為20的元素還要小,表示要查找的元素不是在索引值0的位置上,要不然就是不在序列中;如果要查找的元素比索引值為20的元素還要大,表示要查找的元素可能會出現在索引值為20之後,此時再繼續比較要查找的元素與索引值為20 + i = 2i的元素,i為1, 2, 3, ...。如果在i迭代的過程中發現該索引值對應的元素比要查找的元素還要大時,就可以用二元搜尋法來搜尋索引值2i - 1 + 1 ~ 2i - 1的範圍中,是否有我們要查找的元素;如果序列是有限的,且在i迭代的過程中找不到比要查找的元素還要大的元素,則可以直接用二元搜尋法來搜尋索引值2i - 1 + 1 ~ 序列長度 - 1的範圍。
指數搜尋法的過程
假設現在有個已排序好的整數陣列,內容如下:
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
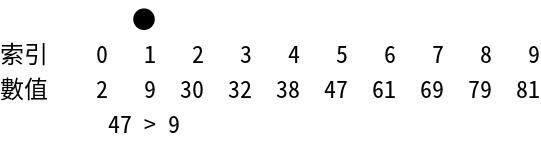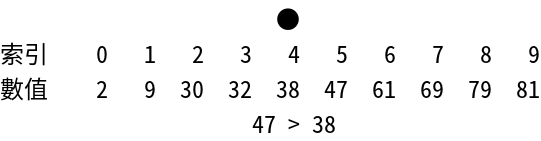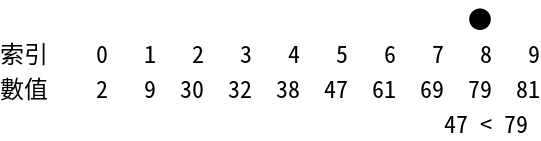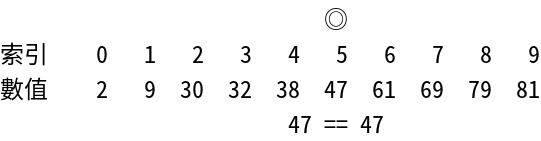
然後我們要用指數搜尋法來找到元素47。一開始先比較索引值為20 = 1的元素和要查找的元素47的大小。
●
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
47 > 9
由於查找的元素47比索引值為20 = 1的元素9還要大,因此繼續與索引值為2i + 1 = 20 + 1 = 21 = 2的元素做比較。
●
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
47 > 30
由於查找的元素47比索引值為21 = 2的元素30還要大,因此繼續與索引值為2i + 1 = 21 + 1 = 22 = 4的元素做比較。
●
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
47 > 38
由於查找的元素47比索引值為22 = 4的元素38還要大,因此繼續與索引值為2i + 1 = 22 + 1 = 23 = 8的元素做比較。
●
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
47 < 79
由於查找的元素47比索引值為23 = 8的元素47還要小,因此我們可以知道如果查找的元素47要存在於該序列中的話,其索引值必定會在22 + 1 ~ 23 - 1的範圍中,也就是5 ~ 7。接著再針對這個範圍做二元搜尋法即可。
● ○ ●
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
47 < 61
◎
索引 0 1 2 3 4 5 6 7 8 9
數值 2 9 30 32 38 47 61 69 79 81
47 == 47
如此一來便可以發現元素47存在序列中索引值為5的位置。若要搜尋的元素在序列中愈前面的話,就可以愈快被搜尋到。
指數搜尋法的程式實作
/// 指數搜尋法。
pub fn exponential_search(array: &[i32], target_element: i32) -> Option<usize> {
let length = array.len();
if length == 0 {
None
} else if target_element == array[0] {
Some(0)
} else {
let mut two = 1;
while two < length {
match target_element.cmp(&array[two]) {
Ordering::Equal => {
return Some(two);
}
Ordering::Less => {
return binary_search(array, target_element, (two >> 1) + 1, two - 1);
}
Ordering::Greater => {
two <<= 1;
}
}
}
binary_search(array, target_element, (two >> 1) + 1, length - 1)
}
}
/// 二元搜尋法,使用迴圈來迭代。
pub fn binary_search(array: &[i32], target_element: i32, mut start: usize, mut end: usize) -> Option<usize> {
while end >= start {
let middle = start + ((end - start) >> 1);
match target_element.cmp(&array[middle]) {
Ordering::Equal => {
return Some(middle);
}
Ordering::Greater => {
start = middle + 1;
}
Ordering::Less => {
if middle > 0 {
end = middle - 1;
} else {
break;
}
}
}
}
None
}
/**
* 指數搜尋法。
*/
public static int exponentialSearch(final int[] array, final int targetElement) {
final int length = array.length;
if (length == 0) {
return -1;
}
if (targetElement == array[0]) {
return 0;
}
int two = 1;
while (two < length) {
if (targetElement == array[two]) {
return two;
} else if (targetElement < array[two]) {
return binarySearch(array, targetElement, (two >> 1) + 1, two - 1);
}
two <<= 1;
}
return binarySearch(array, targetElement, (two >> 1) + 1, length - 1);
}
/**
* 二元搜尋法,使用迴圈來迭代。
*/
public static int binarySearch(final int[] array, final int targetElement, int start, int end) {
while (end >= start) {
final int middle = (end + start) >>> 1;
if (targetElement == array[middle]) {
return middle;
} else if (targetElement > array[middle]) {
start = middle + 1;
} else {
end = middle - 1;
}
}
return -1;
}
/**
* 指數搜尋法。
*/
function exponentialSearch(array: number[], targetElement: number) {
const length = array.length;
if (length === 0) {
return -1;
}
if (targetElement === array[0]) {
return 0;
}
let two = 1;
while (two < length) {
if (targetElement === array[two]) {
return two;
} else if (targetElement < array[two]) {
return binarySearch(array, targetElement, (two >> 1) + 1, two - 1);
}
two <<= 1;
}
return binarySearch(array, targetElement, (two >> 1) + 1, length - 1);
}
/**
* 二元搜尋法,使用迴圈來迭代。
*/
function binarySearch(array: number[], targetElement: number, start: number, end: number) {
while (end >= start) {
const middle = start + ((end - start) >> 1);
if (targetElement === array[middle]) {
return middle;
} else if (targetElement > array[middle]) {
start = middle + 1;
} else {
end = middle - 1;
}
}
return -1;
}
// 指數搜尋法。
func ExponentialSearch(array []int, targetElement int) int {
length := len(array)
if length == 0 {
return -1
}
if targetElement == array[0] {
return 0
}
two := 1
for two < length {
if targetElement == array[two] {
return two
} else if targetElement < array[two] {
return BinarySearch(array, targetElement, (two>>1)+1, two-1)
}
two <<= 1
}
return BinarySearch(array, targetElement, (two>>1)+1, length-1)
}
// 二元搜尋法,使用迴圈來迭代。
func BinarySearch(array []int, targetElement int, start int, end int) int {
for end >= start {
middle := int(uint(end+start) >> 1)
if targetElement == array[middle] {
return middle
} else if targetElement > array[middle] {
start = middle + 1
} else {
end = middle - 1
}
}
return -1
}
左位移一個位元等同於「乘以2」;右位移一個位元等同於「除以2」。
指數搜尋法的複雜度
以#{{n}}#來表示要搜尋的資料筆數。
| 項目 |
值 |
備註 |
| 最差時間複雜度 |
#{{O(\log n)}}# |
|
| 最佳時間複雜度 |
#{{O(1)}}# |
要查找的元素剛好位於序列的最前面。 |
| 平均時間複雜度 |
#{{O(\log n)}}# |
|
| 最差空間複雜度(遞迴的二元搜尋法) |
#{{O(\log n)}}# |
|
| 最差空間複雜度(迭代的二元搜尋法) |
#{{O(1)}}# |
|


