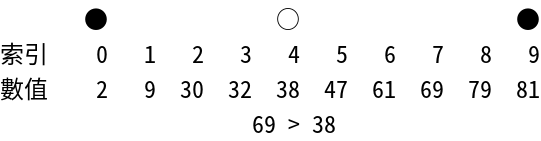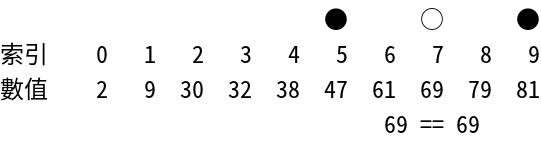
二元搜尋(Binary Search)演算法，簡單又快速的搜尋演算法

二元搜尋(Binary Search)演算法又稱為二分搜尋(Half-Interval Search)演算法或是對數搜尋(Logarithmic Search)演算法，顧名思義，這套演算法的核心思想就在於「二分」，可以在已排序好的序列中進行高效率的搜尋。

二元搜尋法(Binary Search)

二元搜尋法的概念

相對於先前介紹過的線性搜尋法，二元搜尋法不需要把集合中的元素一個一個拿出來判斷，因為它所搜尋的集合必須是已經排序好的序列，所以可以直接利用元素的大小來決定下次要尋找的位置。

在一個已排序好的序列中搜索元素是一件輕鬆容易的事情，我們可以先設定搜索範圍，每次都用這範圍最中間的元素來與要查找的目標元素比大小，如果要查找的目標元素比較大，表示如果目標元素存在於該序列中的話，其一定是位在目前範圍的後半段(值大的那段)；反之，如果要查找的目標元素比較小，表示如果目標元素存在於該序列中的話，其一定是位在目前範圍的前半段(值小的那段)。在下次搜尋的時候，也是一樣拿目標元素與前半段或是後半段的正中央元素進行比較，如此反覆動作，直到找出相同的元素為止；或者直到查找範圍只有一個元素時，表示要找的元素並不存在於序列中。

二元搜尋法的過程

假設現在有個已排序好的整數陣列，內容如下：

索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81

然後我們要用二元搜尋法來找到元素69。這邊可以看到此陣列的長度為10，是偶數，所以並不能剛好選到正中間的元素，不過這也沒關係，選擇索引4或是索引5都可以，在此以索引4為例。

       ●              ○                  ●
索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81
                     69 > 38

由於我們要找的元素69比索引4的元素值38還要來得大，因此可以知道若元素值69存在於該陣列的話，那麼它一定是在索引值大於4的位置，索引值小於4的元素們就都不用去管了。所以下一次搜尋，我們要選擇索引5到索引9的中間元素，也就是索引7。

                           ●      ○      ●
索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81
                                69 == 69

如此一來就找到元素69了，其存在於陣列中的索引7的位置。如何？夠快吧！

二元搜尋法的程式實作

/// 二元搜尋法，使用遞迴。此為用來遞迴呼叫的函數。
pub fn binary_search_recursively(array: &[i32], target_element: i32, start: usize, end: usize) -> Option<usize> {
    if end < start {
        None
    } else {
        let middle = start + ((end - start) >> 1);

        match target_element.cmp(&array[middle]) {
            Ordering::Equal => Some(middle),
            Ordering::Greater => binary_search_recursively(array, target_element, middle + 1, end),
            Ordering::Less => {
                if middle > 0 {
                    binary_search_recursively(array, target_element, start, middle - 1)
                } else {
                    None
                }
            }
        }
    }
}

/// 二元搜尋法，使用遞迴。
pub fn binary_search(array: &[i32], target_element: i32) -> Option<usize> {
    binary_search_recursively(array, target_element, 0, array.len() - 1)
}

>> 1等同於「除以2取整數」，先減後加是為了避免直接計算end + start可能會溢位(超過無號整數的表示範圍，而使得程式panic)。

/**
 * 二元搜尋法，使用遞迴。此為用來遞迴呼叫的函數。
 */
public static int binarySearchRecursively(final int[] array, final int targetElement, final int start, final int end) {
    if (end < start) {
        return -1;
    }

    final int middle = (end + start) >>> 1;

    if (array[middle] == targetElement) {
        return middle;
    } else if (targetElement > array[middle]) {
        return binarySearchRecursively(array, targetElement, middle + 1, end);
    } else {
        return binarySearchRecursively(array, targetElement, start, middle - 1);
    }
}

/**
 * 二元搜尋法，使用遞迴。
 */
public static int binarySearch(final int[] array, final int targetElement) {
    return binarySearchRecursively(array, targetElement, 0, array.length - 1);
}

>>> 1等同於「除以2取整數」，利用無號右位移(unsigned right shift)還可以避免end + start溢位時導致結果錯誤(超過有號正整數的表示範圍，而變成負數)。

/**
 * 二元搜尋法，使用遞迴。此為用來遞迴呼叫的函數。
 */
function binarySearchRecursively(array: number[], targetElement: number, start: number, end: number) {
    if (end < start) {
        return -1;
    }

    const middle = start + ((end - start) >> 1);

    if (array[middle] === targetElement) {
        return middle;
    } else if (targetElement > array[middle]) {
        return binarySearchRecursively(array, targetElement, middle + 1, end);
    } else {
        return binarySearchRecursively(array, targetElement, start, middle - 1);
    }
}

/**
 * 二元搜尋法，使用遞迴。
 */
function binarySearch(array: number[], targetElement: number) {
    return binarySearchRecursively(array, targetElement, 0, array.length - 1);
}

>> 1等同於「除以2取整數」，先減後加是為了避免直接計算end + start可能會超過2³² - 1，若是超過，JavaScript內建的32-bit整數位移功能也就無效了。不過這邊其實也可以寫成(end + start) >>> 1，>>> 1也是等同於「除以2取整數」，但利用無號右位移(unsigned right shift)還可以避免end + start超過2³¹ - 1時進行有號位移(signed shift)後會變成負數的問題，並且又因JavaScript的陣列最大長度是2³¹ - 1，所以end + start在正常情況下並不會超過2³² - 1。

// 二元搜尋法，使用遞迴。此為用來遞迴呼叫的函數。
func BinarySearchRecursively(array []int, targetElement int, start int, end int) int {
	if end < start {
		return -1
	}

	middle := int(uint(end+start) >> 1)

	if array[middle] == targetElement {
		return middle
	} else if targetElement > array[middle] {
		return BinarySearchRecursively(array, targetElement, middle+1, end)
	} else {
		return BinarySearchRecursively(array, targetElement, start, middle-1)
	}
}

// 二元搜尋法，使用遞迴。
func BinarySearch(array []int, targetElement int) (index int) {
	return BinarySearchRecursively(array, targetElement, 0, len(array)-1)
}

>> 1等同於「除以2取整數」，把end+start的結果先轉成無號整數(unsigned integer)是因為它可能會溢位(超過有號正整數的表示範圍，而變成負數)。

在實作程式的時候，應該要避免使用遞迴(Recursive)的結構，因為遞迴需要不斷地重新建構函數的堆疊空間，硬體資源的負擔會比較大，且若是遞迴層數過多還會導致堆疊溢出(Stack Overflow)。所以比較好的做法還是在一個函數內以迴圈迭代的方式來完成。

/// 二元搜尋法，使用迴圈來迭代。
pub fn binary_search(array: &[i32], target_element: i32) -> Option<usize> {
    let mut start = 0;
    let mut end = array.len() - 1;

    while end >= start {
        let middle = start + ((end - start) >> 1);

        match target_element.cmp(&array[middle]) {
            Ordering::Equal => {
                return Some(middle);
            }
            Ordering::Greater => {
                start = middle + 1;
            }
            Ordering::Less => {
                if middle > 0 {
                    end = middle - 1;
                } else {
                    break;
                }
            }
        }
    }

    None
}

或

/// 二元搜尋法，使用標準函式庫(迭代)。
pub fn binary_search(array: &[i32], target_element: i32) -> Option<usize> {
    array.binary_search(&target_element).ok()
}

/**
 * 二元搜尋法，使用迴圈來迭代。
 */
public static int binarySearch(final int[] array, final int targetElement) {
    int start = 0;
    int end = array.length - 1;

    while (end >= start) {
        final int middle = (end + start) >>> 1;

        if (targetElement == array[middle] ) {
            return middle;
        } else if (targetElement > array[middle]) {
            start = middle + 1;
        } else {
            end = middle - 1;
        }
    }

    return -1;
}

或

/**
 * 二元搜尋法，使用標準函式庫(迭代)。
 */
public static int binarySearch(final int[] array, final int targetElement) {
    final int index = Arrays.binarySearch(array, targetElement);

    if (index < 0) {
        return -1;
    }

    return index;
}

/**
 * 二元搜尋法，使用迴圈來迭代。
 */
function binarySearch(array: number[], targetElement: number) {
    let start = 0;
    let end = array.length - 1;

    while (end >= start) {
        const middle = start + ((end - start) >> 1);

        if (targetElement === array[middle]) {
            return middle;
        } else if (targetElement > array[middle]) {
            start = middle + 1;
        } else {
            end = middle - 1;
        }
    }

    return -1;
}

// 二元搜尋法，使用迴圈來迭代。
func BinarySearch(array []int, targetElement int) int {
	start := 0
	end := len(array) - 1

	for end >= start {
		middle := int(uint(end+start) >> 1)

		if targetElement == array[middle] {
			return middle
		} else if targetElement > array[middle] {
			start = middle + 1
		} else {
			end = middle - 1
		}
	}

	return -1
}

或

// 二元搜尋法，使用標準函式庫(迭代)。
func BinarySearch(array []int, targetElement int) int {
	length := len(array)

	index := sort.Search(length, func(i int) bool {
		return array[i] >= targetElement
	})

	if index < length && array[index] == targetElement {
		return index
	} else {
		return -1
	}
}

二元搜尋法的複雜度

以#{{n}}#來表示要搜尋的資料筆數。

項目	值	備註
最差時間複雜度	#{{O(\log n)}}#	元素不在序列中，或者是二分到不能再分時才被發現。
最佳時間複雜度	#{{O(1)}}#	要查找的元素剛好位於序列的中間。
平均時間複雜度	#{{O(\log n)}}#
最差空間複雜度(遞迴)	#{{O(\log n)}}#
最差空間複雜度(迭代)	#{{O(1)}}#