一個物體要從一端移動到另一端,首先它必須要先到達路程的二分之一,而它為了要先到達路程的二分之一,它也必須先到達路程的四分之一。依此類推,物體要移動到某一個位置,它總是必須要先完成該路程的一半的路程,所以會有無限的路程要走。於是我們可以得到一個結論──物體要運動是不可能的事!
這個理論是古希臘哲學家Zeno of Elea(芝諾)所提出的,讓我們來實際用數學式子看看他到底說得對不對吧!
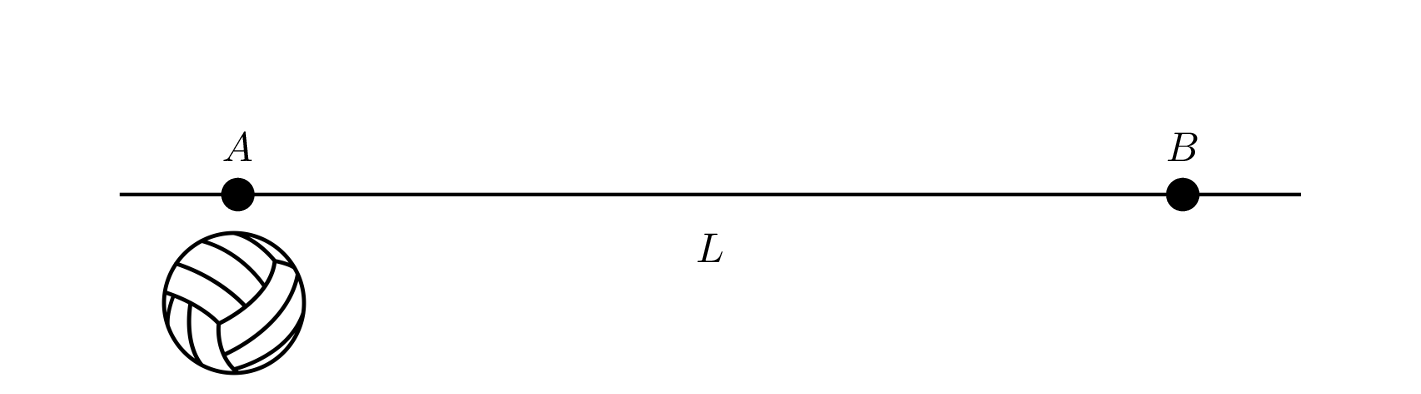
若一個物體要從#{{A}}#移動到距離#{{L}}#的位置#{{B}}#,示意圖如下:
假設這個物體的移動速度為#{{V}}#,且#{{V > 0}}#,則這個物體從#{{A}}#移動到#{{B}}#的時間為:
#{{{ t = { L \over V } }}}#
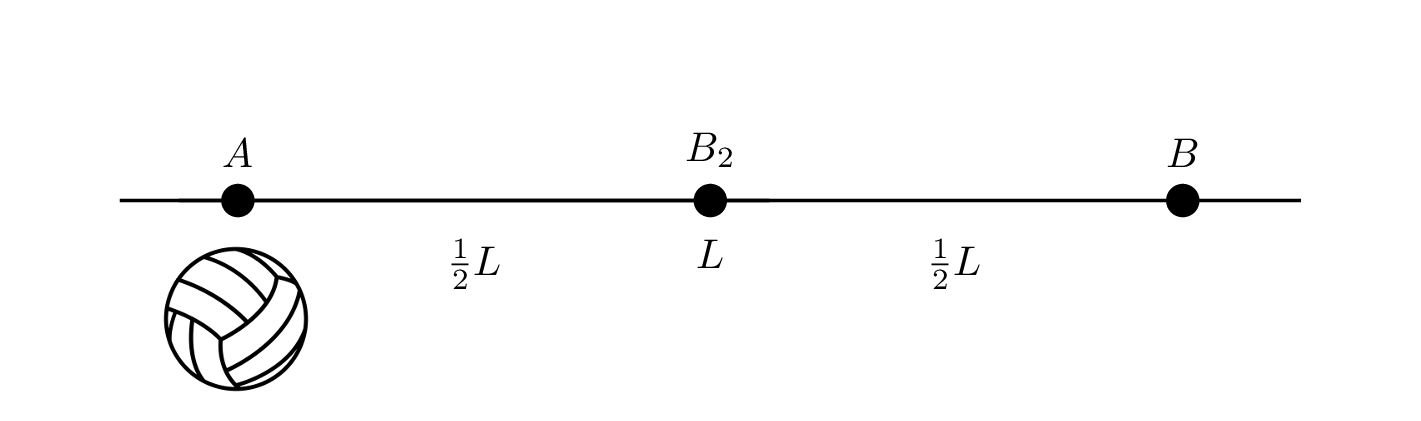
這個物體為了要從#{{A}}#移動到#{{B}}#,它必須要先移動到#{{ {1 \over 2}L }}#的位置#{{B_{2}}}#,所須花費的時間為#{{ {1 \over 2}t }}#。示意圖如下:
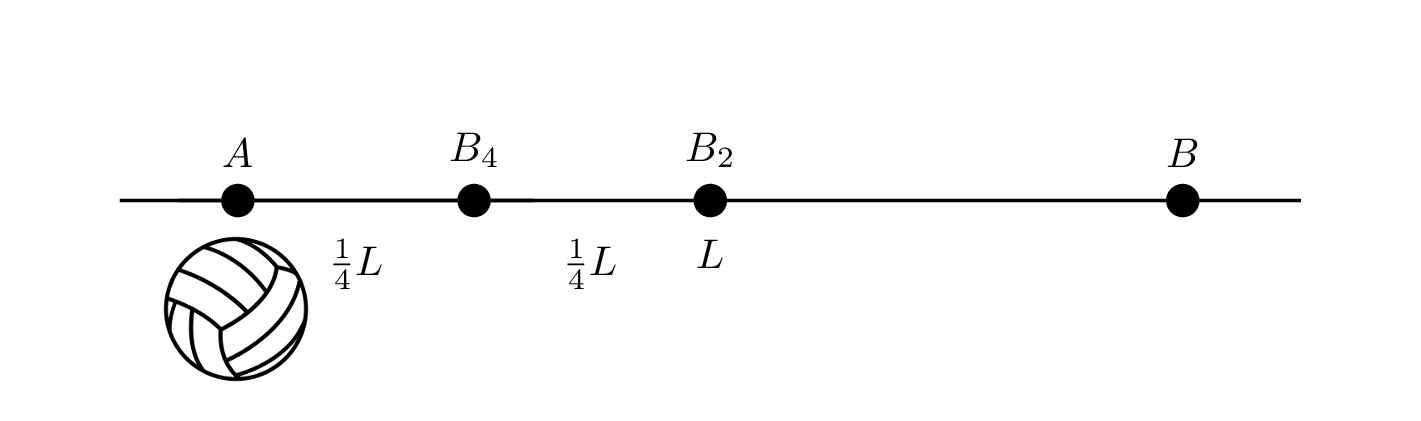
這個物體為了要從#{{A}}#移動到#{{B_{2}}}#,它必須要先移動到#{{ {1 \over 4}L }}#的位置#{{B_{4}}}#,所須花費的時間為#{{ {1 \over 4}t }}#。示意圖如下:
也就是說,總路程#{{L}}#可以拆解成:
#{{{
\begin{eqnarray}
L &=& { 1 \over 2 }L + { 1 \over 4 }L + { 1 \over 8 }L + { 1 \over 16 }L + \cdots \nonumber \\
&=& ({ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots)L
\end{eqnarray}
}}}#
所以所需時間,
#{{{
\begin{eqnarray}
t &=& { {({ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots)L} \over V } \nonumber \\
&=& { {({ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots)} {L \over V} } \nonumber \\
&=& { {({ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots)} t }
\end{eqnarray}
}}}#
接著我們會需要證明#{{ ({ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots) }}#是否#{{ = 1 }}#。如果是的話,表示芝諾提出的這個理論,「運動是不可能的」這個結論是錯的;如果不是的話,表示芝諾提出的這個理論確實是古怪的悖論。
利用結合率,先將式子改成:
#{{{
{ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots \nonumber \\
\begin{eqnarray}
&=& (1 - { 1 \over 2 }) + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots \nonumber \\
&=& [(1 - { 2 \over 4 }) + { 1 \over 4 }] + { 1 \over 8 } + { 1 \over 16 } + \cdots \nonumber \\
&=& (1 - { 1 \over 4 }) + { 1 \over 8 } + { 1 \over 16 } + \cdots \nonumber \\
&=& [(1 - { 2 \over 8 }) + { 1 \over 8 }] + { 1 \over 16 } + \cdots \nonumber \\
&=& (1 - { 1 \over 8 }) + { 1 \over 16 } + \cdots \nonumber \\
& & \cdots
\end{eqnarray}
}}}#
以極限#{{\lim}}#表示的話:
#{{{
\begin{eqnarray}
{ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots &=& \lim_{n \to \infty} (1 - { 1 \over 2^n }) \nonumber \\
&=& 1
\end{eqnarray}
}}}#
#{{ ({ 1 \over 2 } + { 1 \over 4 } + { 1 \over 8 } + { 1 \over 16 } + \cdots) = 1 }}#得證,所以二分法悖論只能說是一個謬論,是當時的人們還沒有很清楚地「極限」或是「無窮」的概念,認為用這樣的方式來思考這個運動問題的話,問題就似乎會變得無解。