一片雪花的周長比地球直徑還要長，面積卻比一枚硬幣還要小！？

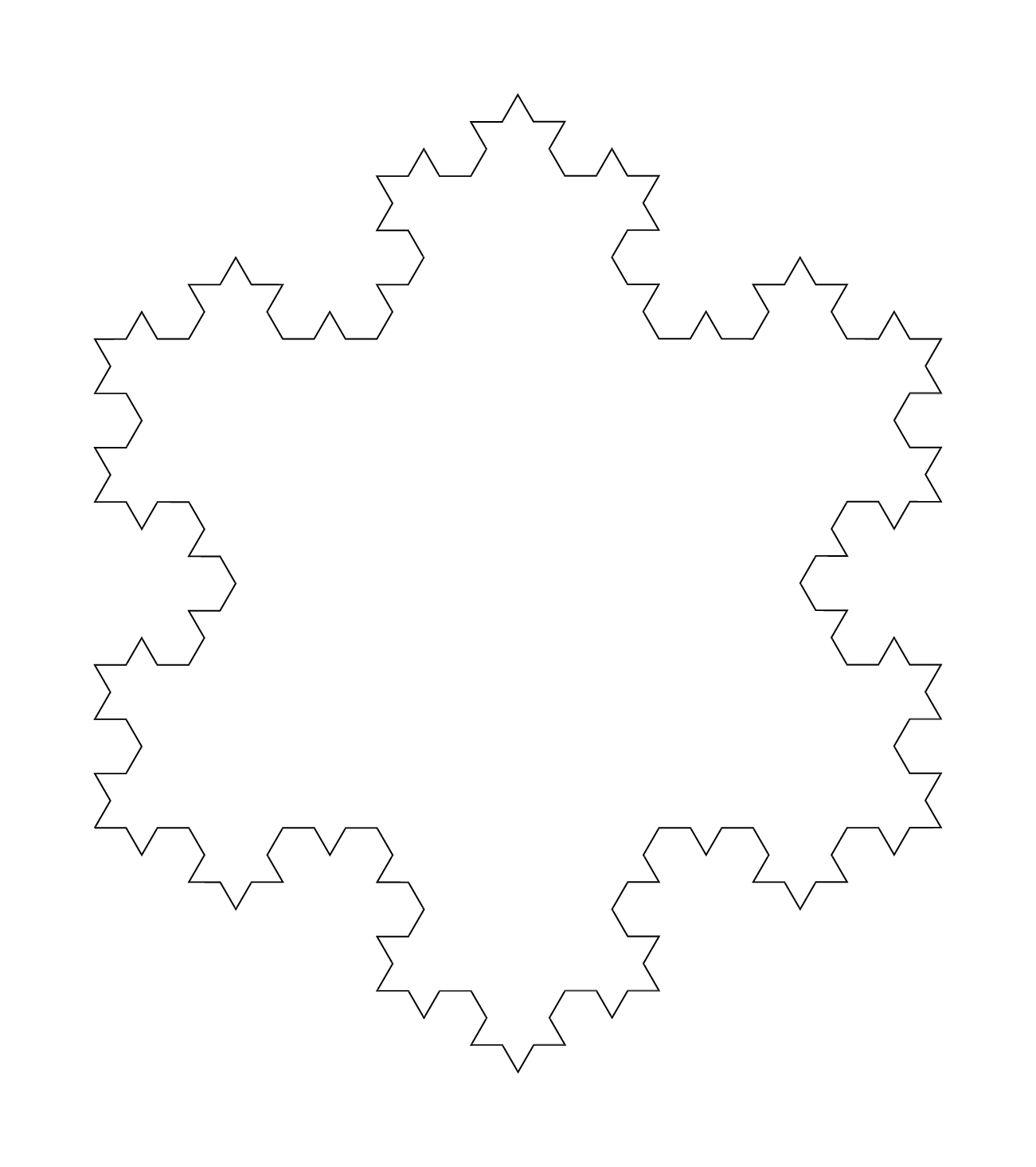
在計算雪花的周長和面積之前，我們必須先知道雪花到底是什麼「形狀」。自然界產生的雪花，因水分子#{{H_{2}O}}#在結合成固態水(冰)的排列方式的影響，大部份是以六邊形為基礎，但也由於形成時的條件不同，而導致產生出來的雪花幾乎每個都長的不一樣，形狀甚至有好幾十種。在此我們只會探討最理想的形狀，也就是俗稱為雪花曲線的「科赫曲線」(Koch curve)。

科赫曲線

假設有一個邊長為#{{L}}#的正三角形。示意圖如下：

接將三角形每個邊切成三等分，在#{{ {1 \over 3}L }}#和#{{ {2 \over 3}L }}#處向外再做一個邊長為#{{ {1 \over 3}L }}#的正三角形。示意圖如下：

依此類推，持續把所有的邊切成三等分，製造更多的正三角形出來。示意圖如下：

這樣的形狀稱作「碎形」(fractal)。碎形有一個非常有趣的特性，那就是我們可以取其中任一個部份放大來看，還會是原來的形狀。示意圖如下：

科赫曲線的周長

那麼究竟要怎麼替這種奇怪的形狀計算周長呢？若正三角形的邊長為#{{L}}#，則此正三角形的周長為#{{3L}}#。科赫曲線迭代一次，每個邊的長度就會是原先的#{{4 \over 3}}#倍。因此，科赫曲線圖形的周長為：

#{{{
3L \times {({4 \over 3} \times {4 \over 3} \times {4 \over 3} \times \cdots)} \to \infty
}}}#

我們可以算出周長是趨近於無窮大的結果，而地球的直徑大約是12742公里，因此一片理想的雪花，其周長會遠遠超過地球的直徑！

科赫曲線的面積

既然科赫曲線的圖形周長無限大，面積難道不也是無限大嗎？若正三角形的邊長為#{{L}}#，則此正三角形的面積為#{{ {{\sqrt 3} \over 4}L^2 = A }}#。科赫曲線迭代第一次，每個邊上就會多出一個邊長為#{{ {1 \over 3}L }}#，也就是面積為#{{ {1 \over 9}A }}#的正三角形，數量有3個。接著再迭代第二次，每個邊上就會多出一個邊長為#{{ {1 \over 9}L }}#，也就是面積為#{{ {1 \over 81}A }}#的正三角形，數量有12個。接著再迭代第三次，每個邊上就會多出一個邊長為#{{ {1 \over 27}L }}#，也就是面積為#{{ {1 \over 729}A }}#的正三角形，數量有48個。因此，科赫曲線圖形的面積為：

#{{{
\begin{eqnarray}
A \text{ } &+& ({3 \times 4^0})({1 \over 9^1}A) \nonumber \\
&+& ({3 \times 4^1})({1 \over 9^2}A) \nonumber \\
&+& ({3 \times 4^2})({1 \over 9^3}A) \nonumber \\
&+& \cdots
\end{eqnarray}
}}}#

以總和#{{\sum}}#和極限#{{\lim}}#表示的話：

#{{{
\begin{eqnarray}
A + \sum_{n \to \infty} ({3 \times 4^{n-1}} {1 \over {9^n}}) = A + 3A \sum_{n \to \infty} ( {{4^{n-1}} \over {9^n}} )
\end{eqnarray}
}}}#

#{{{
\begin{eqnarray}
\sum_{n \to \infty} ( {{4^{n-1}} \over {9^n}} ) &=& \sum_{n \to \infty} ( {1 \over 9} \times {{4^{n-1}} \over {9^{n-1}}} ) \nonumber \\
&=& {1 \over 9} \sum_{n \to \infty} ({ 4 \over 9 })^{n-1} \nonumber \\
&=& {1 \over 9} \times {{1 - \lim\limits_{n \to \infty} { ({4 \over 9})^n} } \over {1 - {4 \over 9} } } \nonumber \\
&=& {1 \over 9} \times {1 \over { 5 \over 9 } } \nonumber \\
&=& 1 \over 5
\end{eqnarray}
}}}#

所以面積為：

#{{{
A + {3 \over 5}A = {8 \over 5}A = {8 \over 5} \times {{\sqrt 3} \over 4}L^2 = {2{\sqrt 3} \over 5}L^2
}}}#

假設這個雪花的L為4毫米，面積則約為#{{ {2{\sqrt 3} \over 5} \times {4^2} = 11 }}#平方毫米，而一枚新台幣1元硬幣面積為#{{ \pi \times {10^2} \approx 314}}#平方毫米，所以硬幣的面積大於周長比地球直徑還要長的雪花的面積！