理論上,喀答聲(Click)應該只會發生在頻率急遽改變或是振幅急遽改變的時候。但實際上,只要波形有發生任何一點不連續(就算不連續的地方只有0.000001秒),就會產生喀答聲。要消除振幅或是頻率改變產生的喀答聲,雖可以使用波形包絡,但若是固定的振幅和固定的頻率所產生的喀答聲,就得另外用別種方式了。
固定的振幅和固定的頻率怎麼會產生喀答聲呢?請先看看以下的例子,使用同一種樂器、同一種音調、在連續的時間裡演奏同樣長度的音符。
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100 ;sample rate
ksmps = 1 ;samples in a control period
nchnls = 1 ;number of channels
0dbfs = 100 ;value of 0db
instr 1
;p4=freq
;p3=duration
iamp = ampdb(p4) ;convert decibels to linear amp
ifreq = cpspch(p4) ;convert pitch to frequent
a1 oscil 100, ifreq, 1 ;oscillate f1
out a1 ;output
endin
</CsInstruments>
<CsScore>
f1 0 16384 10 1
t 0 60
;ins strt dur pitch
i1 0 1 8.00
i1 + 1 8.00
i1 + 1 8.00
i1 + 1 8.00
e
</CsScore>
</CsoundSynthesizer>
音樂檔下載
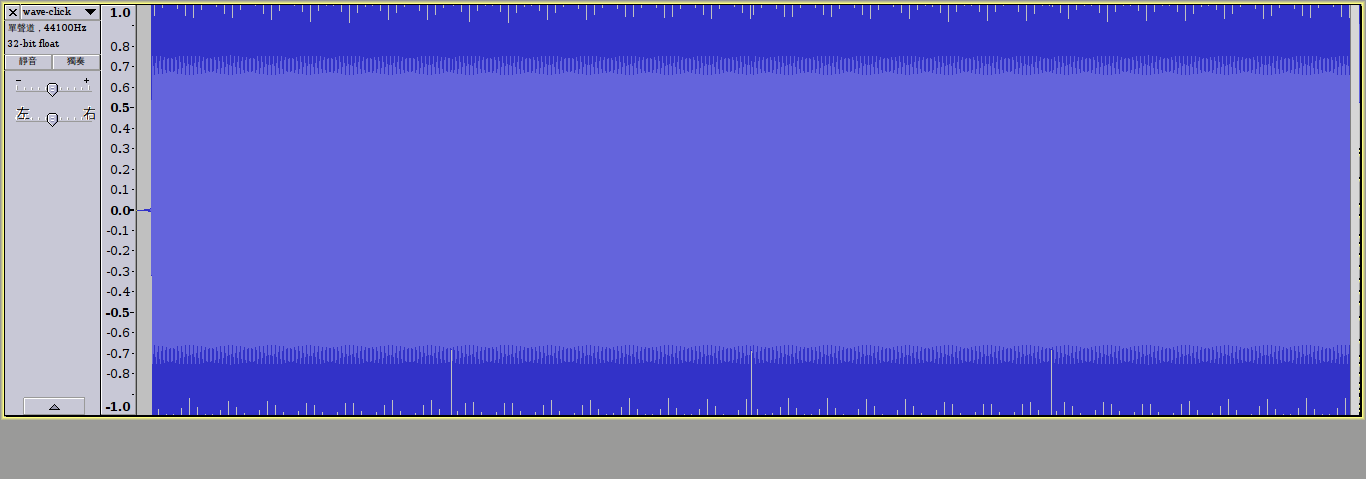
這段聲音,是由正弦波產生出來的C4音,一共產生了四次。由於這個樂器沒有做波形包絡,演奏四個音符會產生五個喀答聲,這不是本來就會這樣嗎?不!起始和結尾有喀答聲是很正常沒錯,但是每個音符之間既然振幅和頻率都一樣,又怎麼會出現喀答聲呢!?答案就是這些音符之間的波形並沒有被完美接合的關係,先來看看波形吧!
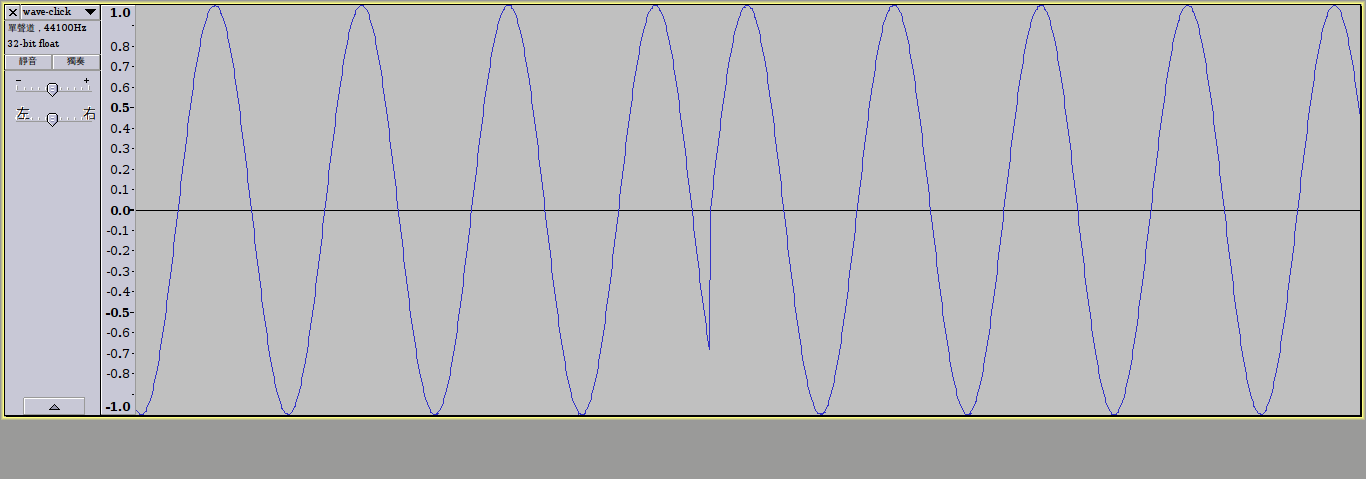
從聲紋圖中可以發現,音符和音符之間,居然產生了明顯的斷層。看得更仔細一點,如下圖:
正弦波真的斷掉了!
究竟是什麼原因造成這種情況呢?答案就是頻率啦!我們在演奏Pitch 8.00(相當於C4)的時候,實際上是使用約261.6Hz這樣的頻率去振盪波形,如果演奏1秒的C4,那麼就會有261.6個波形週期,問題就是出現在這最後的.6!因為音符在最後的時候,無法產生出完整的全波,所以與下一個音符接續的時候,就會造成不連續的現象,因此我們必須要微調頻率,使得這個長度時間下的這個頻率能夠在音符結尾的時候,以完美的全波結束。
若要都用全波來塞滿某時間長度的話,必須在時間內振盪出整數的波形週期,如果時間是1秒,那頻率就一定是整數;如果時間是2秒,那頻率就一定是0.5的倍數。因此可以推導出近似頻率的演算法如下:
全波數量=時間/週期=時間*頻率
強制將全波數量近似於一個整數值
頻率=全波數量/時間
如此一來便可以得到能夠在時間內振盪出完整由全波組成的波形的頻率了!
因此若將上面的Csound程式改寫如下,就可以有效的消除喀答聲。
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100 ;sample rate
ksmps = 1 ;samples in a control period
nchnls = 1 ;number of channels
0dbfs = 100 ;value of 0db
instr 1
;p4=freq
;p3=duration
iamp = ampdb(p4) ;convert decibels to linear amp
ifreq = cpspch(p4) ;convert pitch to frequent
;Modify freq to avoid click
iFreqRadio = round (ifreq*p3)
ifreq = iFreqRadio/p3
a1 oscil 100, ifreq, 1 ;oscillate f1
out a1 ;output
endin
</CsInstruments>
<CsScore>
f1 0 16384 10 1
t 0 60
;ins strt dur pitch
i1 0 1 8.00
i1 + 1 8.00
i1 + 1 8.00
i1 + 1 8.00
e
</CsScore>
</CsoundSynthesizer>