所謂的密鋪(tessellation)是用一種或多種平面形狀去填滿一個更大的平面。用正六邊形(regular hexagon)來密鋪成網格(grid),會比用矩形密鋪還來得更複雜,造成更藝術的視覺效果。那麼要如何寫程式來畫出這個複雜的正六邊形網格呢?
正六邊形,有六個等長的邊和六個相等的內角,每個內角都是#{{ {360^\circ \over 6} = 60^\circ }}#。一個平面形狀要有平面密鋪的能力,其平鋪後每個交接點的任意兩相鄰的邊所形成的夾角和必須要能是#{{360^\circ}}#,在正多邊形中,只有正三邊形、正四邊形、正六邊形能夠密鋪。
在繪製正六邊形網格前要先會繪製正六邊形,可以參考這篇文章:
接著還要了解一下正六邊形各個部份的長度。
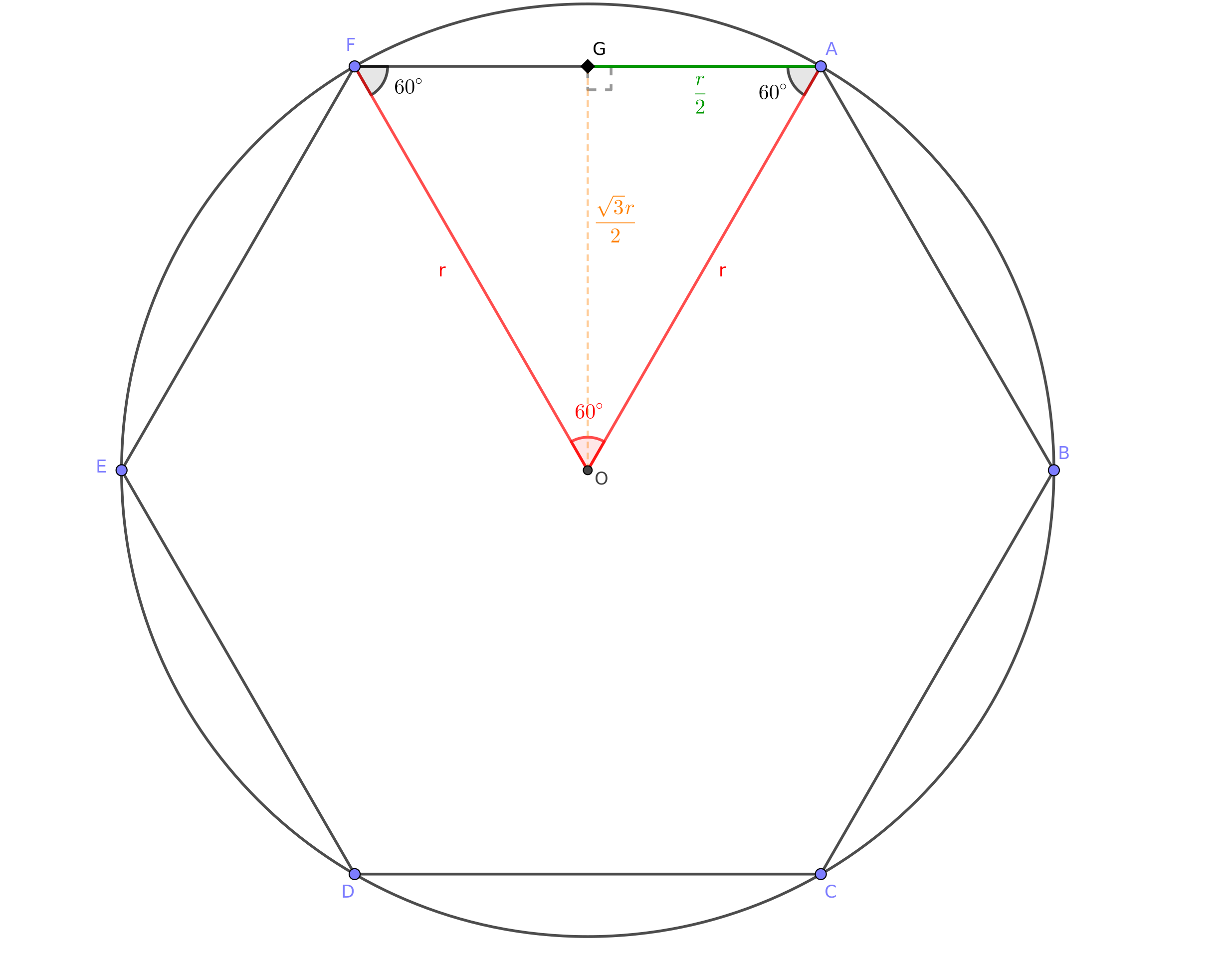
如上圖,#{{ \overline{OA} }}#是圓#{{O}}#的半徑#{{r}}#,即為這個六邊形#{{ABCDEF}}#的外接圓半徑(circumradius)。由於#{{\angle{AOF} = 60^\circ}}#,且#{{ \overline{OA} = \overline{OF} }}#,所以#{{ \angle{FAO} = \angle{OFA} }}#,所以#{{ \triangle{AOF} }}#是正三角形,可以知道#{{ \overline{FA} = \overline{OA} = r }}#。設#{{G}}#為#{{ \overline{FA} }}#的中點,則#{{ \overline{GA} = {\overline{FA} \over 2 } = {r \over 2} }}#。#{{ \triangle{AOG} }}#是直角三角形,根據勾股定理,直角三角形的兩股長的平方和等於斜邊的平方,可列出#{{ \overline{OG}^2 = r^2 - {r^2 \over 4} = {3r^2 \over 4} }}#,所以#{{ \overline{OG} = {\sqrt{3}r \over 2} }}#。#{{ \overline{OG} }}#即為這個六邊形#{{ABCDEF}}#的內切圓半徑(inradius)。
再來看看正六邊形密鋪的樣子,如下圖:
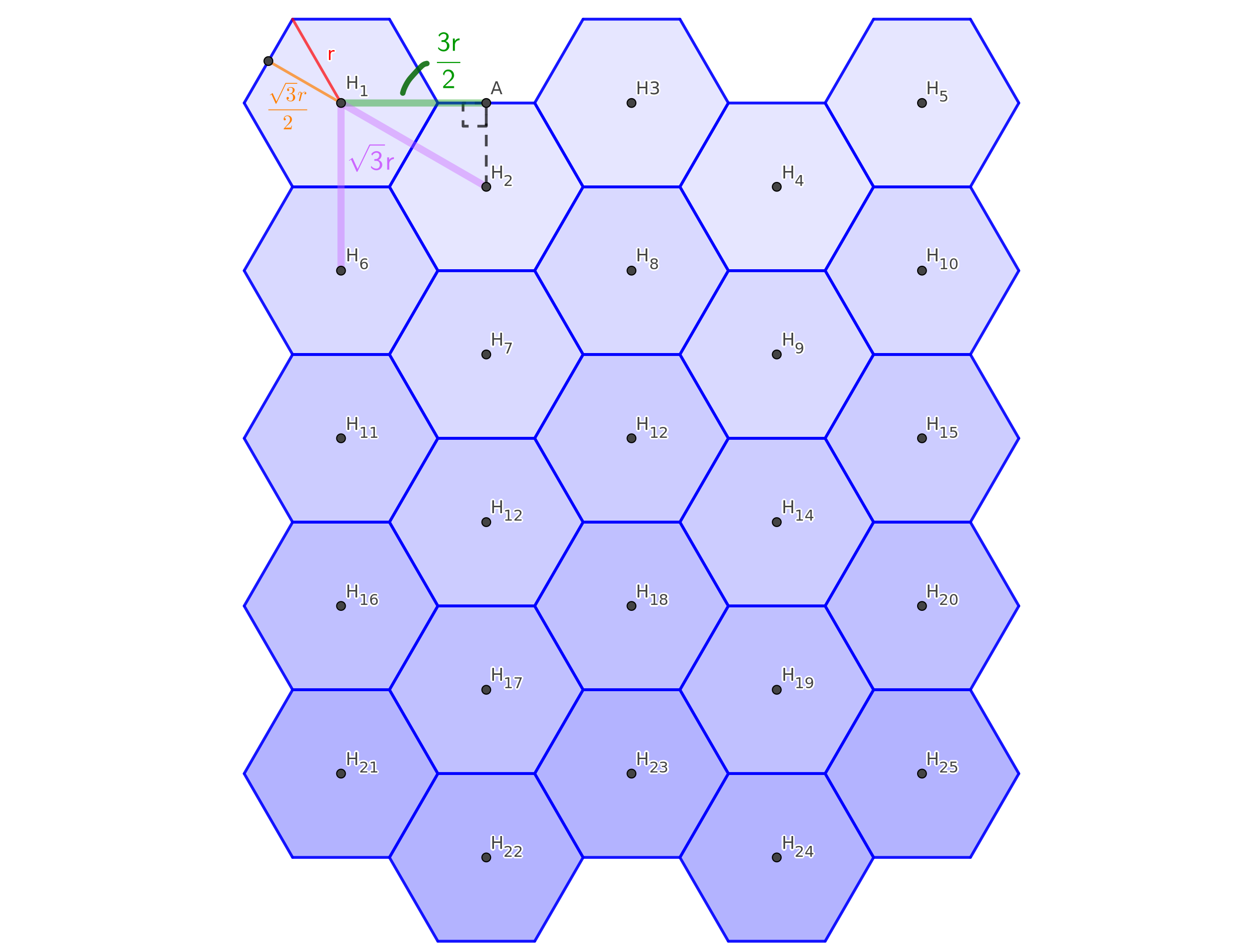
上圖是一個#{{ 5 \times 5 }}#的正六邊形網格,其中的點#{{H_i}}#是各個正六邊形的中心,#{{i}}#將正六邊從左到右、從上到下按順序編號。觀察後可以知道,水平相鄰的正六邊形,中心點相隔了#{{ 3r \over 2 }}#的水平距離;垂直相鄰的正六邊形,中心點相隔了#{{ \sqrt{3}r }}#的垂直距離。
掌握了這些資訊後,只要去計算正六邊形網格的正六邊形中心點的位置,再用繪製正多邊形的方法在那個位置上畫出正六邊形就可以繪製出正六邊形網格了。
以網頁瀏覽器上的JavaScript為例,可以寫出如下的程式:
const canvas = document.getElementById("hexagon-grid");
const drawHexagonGrid = (width = 5, height = 5, margin = 5) => {
if (canvas.getContext) {
const ctx = canvas.getContext("2d");
canvas.width = canvas.clientWidth;
canvas.height = canvas.clientHeight;
/*
// clear the canvas; it might not be necessary because the size of the canvas has been re-assigned and thus the canvas should have been cleared
ctx.clearRect(
0,
0,
canvas.width,
canvas.height,
);
*/
width = Math.floor(width); // ensure width is an integer
height = Math.floor(height); // ensure height is an integer
if (width < 1 || height < 1) {
return;
}
const marginTwice = margin * 2;
const gridMaxWidth = canvas.width - marginTwice; // = r * (3 / 2) * (width - 1)
const gridMaxHeight = canvas.height - marginTwice; // = (sqrt(3) * r) * (height - 0.5)
const widthDec = width - 1;
const heightDecOneHalf = height - 0.5;
const SQRT3 = Math.sqrt(3);
const wr = gridMaxWidth / 1.5 / widthDec;
const hr = gridMaxHeight / SQRT3 / heightDecOneHalf;
const r = Math.min(wr, hr); // circumradius
const dw = r * 1.5;
const dh = SQRT3 * r;
const dhHalf = dh / 2; // inradius
const gridWidth = dw * widthDec;
const gridHeight = dh * heightDecOneHalf;
const ox = (canvas.width - gridWidth) / 2;
const oy = (canvas.height - gridHeight) / 2;
const angle = 2.0 * Math.PI / 6;
const points = new Array(6);
for (let i = 0;i < 6;i++) {
const a = angle * i;
const px = Math.cos(a) * r;
const py = Math.sin(a) * r;
points[i] = [px, py];
}
const drawLine = (centerPoint, a, b) => {
ctx.beginPath();
ctx.moveTo(centerPoint[0] + a[0], centerPoint[1] + a[1]);
ctx.lineTo(centerPoint[0] + b[0], centerPoint[1] + b[1]);
ctx.stroke();
};
const drawHexagon = (centerPoint) => {
for (let i = 5;i > 0;i--) {
drawLine(centerPoint, points[i], points[i - 1]);
}
drawLine(centerPoint, points[0], points[5]);
};
for (let h = 0;h < height;h++) {
const y = oy + (h * dh);
for (let w = 0;w < width;w += 2) {
drawHexagon([ox + (w * dw), y]);
}
const yy = y + dhHalf;
for (let w = 1;w < width;w += 2) {
drawHexagon([ox + (w * dw), yy]);
}
}
}
};
以上程式的canvas常數是HTML中ID為hexagon-grid的canvas元素。if (canvas.getContext)是在判斷網頁瀏覽器有無支援canvas元素。
canvas元素能夠完全容得下#{{ width \times height }}#的正六邊形網格。
程式第79到91行是在計算每個正六邊形的中心點位置,並在那個位置繪製正六邊形。
當width等於1時,以上程式會畫出比較奇怪的結果。我們可以把程式修改成以下的樣子:
const canvas = document.getElementById("hexagon-grid");
const drawHexagonGrid = (width = 5, height = 5, margin = 5) => {
if (canvas.getContext) {
const ctx = canvas.getContext("2d");
canvas.width = canvas.clientWidth;
canvas.height = canvas.clientHeight;
/*
// clear the canvas; it might not be necessary because the size of the canvas has been re-assigned and thus the canvas should have been cleared
ctx.clearRect(
0,
0,
canvas.width,
canvas.height,
);
*/
const angle = 2.0 * Math.PI / 6;
const points = new Array(6);
const drawLine = (centerPoint, a, b) => {
ctx.beginPath();
ctx.moveTo(centerPoint[0] + a[0], centerPoint[1] + a[1]);
ctx.lineTo(centerPoint[0] + b[0], centerPoint[1] + b[1]);
ctx.stroke();
};
const drawHexagon = (centerPoint) => {
for (let i = 5;i > 0;i--) {
drawLine(centerPoint, points[i], points[i - 1]);
}
drawLine(centerPoint, points[0], points[5]);
};
const initializePoints = (r) => {
for (let i = 0;i < 6;i++) {
const a = angle * i;
const px = Math.cos(a) * r;
const py = Math.sin(a) * r;
points[i] = [px, py];
}
};
width = Math.floor(width); // ensure width is an integer
height = Math.floor(height); // ensure height is an integer
const marginTwice = margin * 2;
const gridMaxWidth = canvas.width - marginTwice;
const gridMaxHeight = canvas.height - marginTwice;
const SQRT3 = Math.sqrt(3);
if (width < 1 || height < 1) {
return;
}
if (width === 1) {
const wr = gridMaxWidth;
const hr = gridMaxHeight / SQRT3 / height;
const r = Math.min(wr, hr); // circumradius
const dh = SQRT3 * r;
const dhHalf = dh / 2; // inradius
const gridWidth = r;
const gridHeight = dh * height;
const ox = ((canvas.width - gridWidth) / 2) + (r / 2);
const oy = ((canvas.height - gridHeight) / 2) + dhHalf;
initializePoints(r);
for (let h = 0;h < height;h++) {
drawHexagon([ox, oy + (h * dh)]);
}
return;
}
const widthDec = width - 1;
const heightDecOneHalf = height - 0.5;
const wr = gridMaxWidth / 1.5 / widthDec;
const hr = gridMaxHeight / SQRT3 / heightDecOneHalf;
const r = Math.min(wr, hr); // circumradius
const dw = r * 1.5;
const dh = SQRT3 * r;
const dhHalf = dh / 2; // inradius
const gridWidth = dw * widthDec;
const gridHeight = dh * heightDecOneHalf;
const ox = (canvas.width - gridWidth) / 2;
const oy = (canvas.height - gridHeight) / 2;
initializePoints(r);
for (let h = 0;h < height;h++) {
const y = oy + (h * dh);
for (let w = 0;w < width;w += 2) {
drawHexagon([ox + (w * dw), y]);
}
const yy = y + dhHalf;
for (let w = 1;w < width;w += 2) {
drawHexagon([ox + (w * dw), yy]);
}
}
}
};