N邊形,有N個頂點、N個邊。每個邊都是由兩個頂點連線組成,因此只要找到多邊形的各頂點座標,就可以輕易地連線畫出多邊形了!而所謂的正多邊形,它的邊都是等長的,且任意相鄰兩邊之間所形成的夾角也都是相等的。
要找到正多邊形的頂點,我們可以利用「圓」來內接正多邊形。在繪製正N邊形的時候,可以將圓周平均切分出N個頂點,這N個頂點即可連成正多邊形。
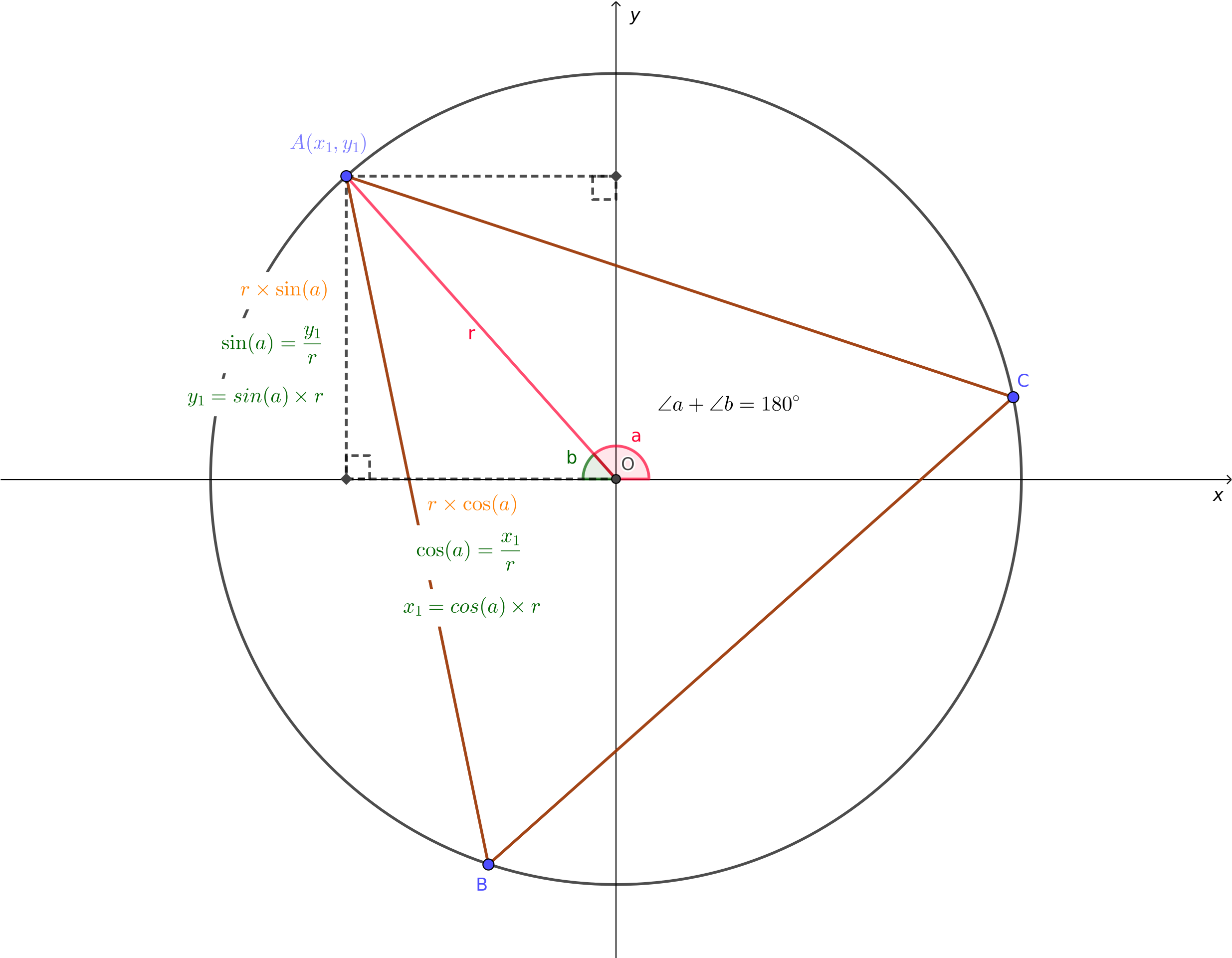
如下圖:
一個圓的弧度為#{{2\pi}}#。若要在半徑為#{{r}}#的圓內繪製出一個正三角形,可以利用弧度#{{ {2\pi} \over 3 }}#將圓周切成三等分,最後利用三角函數#{{ \sin{\theta} = {對邊 \over 斜邊} }}#、#{{ \cos{\theta} = {鄰邊 \over 斜邊} }}#來求得圓周上頂點的座標。
在上圖中,圓心定在#{{O(0, 0)}}#方便計算。至於為什麼是用#{{ \sin{(a)} }}#、#{{ \cos{(a)} }}#而不是#{{ \sin{(b)} }}#、#{{ \cos{(b)} }}#,是因為頂點A位在第二象限,此時#{{ \sin{(a)} = \sin{(180^\circ - a)} = \sin{(b)} }}#,#{{ \cos{(a)} = -\cos{(180^\circ - a)} = -\cos{(b)} }}#。要算其它象限的頂點也是類似的概念,直接用#{{ \angle{a} }}#去算即可。
設N邊形有#{{N}}#個頂點,分別是#{{P_{i}(x_i, y_i), \text{where } i = 0, 1, \dots, N - 1}}#。則:
#{{{
x_i = cos(i \times {{2\pi} \over N}) \times r
}}}#
#{{{
y_i = sin(i \times {{2\pi} \over N}) \times r
}}}#
有了公式,就可以開始撰寫程式碼了。以網頁瀏覽器上的JavaScript為例,可以寫出如下的程式:
const canvas = document.getElementById("regular-polygon");
const drawPolygon = (
n = 3,
angleOffset = 0,
edge = true,
diagonal = true,
margin = 0,
) => {
if (canvas.getContext) {
const ctx = canvas.getContext("2d");
canvas.width = canvas.clientWidth;
canvas.height = canvas.clientHeight;
/*
// clear the canvas; it might not be necessary because the size of the canvas has been re-assigned and thus the canvas should have been cleared
ctx.clearRect(
0,
0,
canvas.width,
canvas.height,
);
*/
if (n < 3 || n > 99) {
return;
}
n = Math.floor(n); // ensure n is an integer
const centerPoint = [canvas.width / 2, canvas.height / 2];
const r = Math.min(...centerPoint) - (margin * 2);
const points = new Array(n);
const angle = 2.0 * Math.PI / n;
for (let i = 0;i < n;i++) {
const a = angleOffset + (angle * i);
const px = Math.cos(a) * r;
const py = Math.sin(a) * r;
points[i] = [px, py];
}
const drawLine = (a, b) => {
ctx.beginPath();
ctx.moveTo(centerPoint[0] + a[0], centerPoint[1] - a[1]);
ctx.lineTo(centerPoint[0] + b[0], centerPoint[1] - b[1]);
ctx.stroke();
};
if (edge) {
for (let i = n - 1;i > 0;i--) {
drawLine(points[i], points[i - 1]);
}
drawLine(points[0], points[n - 1]);
}
if (diagonal) {
const pointA = points[n - 1];
for (let j = n - 3;j > 0;j--) {
drawLine(pointA, points[j]);
}
for (let i = n - 2;i > 0;i--) {
const pointA = points[i];
for (let j = i - 2;j >= 0;j--) {
drawLine(pointA, points[j]);
}
}
}
}
};
以上程式的canvas常數是HTML中ID為regular-polygon的canvas元素。if (canvas.getContext)是在判斷網頁瀏覽器有無支援canvas元素。
由於HTML的canvas元素的y軸方向和我們熟知的y軸向上的直角坐標系是相反的,所以在drawLine的時候把y值反過來計算