插補搜尋(Interpolation Search)演算法，運用資料近似線來輔助搜尋的演算法

插補搜尋法(Interpolation Search)

插補搜尋法的概念

插補搜尋法是基於二元搜尋法的演算法，如果您還不了解二元搜尋法的話，請先參考這篇文章：

插補搜尋法不像二元搜尋法每次都選擇序列搜尋範圍的中間元素，而是藉由目前搜尋範圍的近似線公式來導出要搜尋的元素可能會存在或是可能比較接近的索引位置。舉例來說，若我們知道該搜尋範圍的序列資料可以用直線方程式#{{ y = x + 1 }}#來表示的話，其中#{{y}}#是元素值，#{{x}}#是索引值，那麼我們可以利用要查找的元素值#{{y}}#來直接計算出其索引值#{{x}}#，#{{x = y - 1}}#，如此一來這個序列的搜尋時間複雜度就會是#{{O(1)}}#。

當然，現實中的資料不太可能都剛好是線性的。所以我們會使用「線性近似」的手段，選取幾個點來計算出資料的近似線，在這線段上的資料即為內插。內插值雖然可能不會剛好是原始的資料值，但至少可以接近原始的資料值。

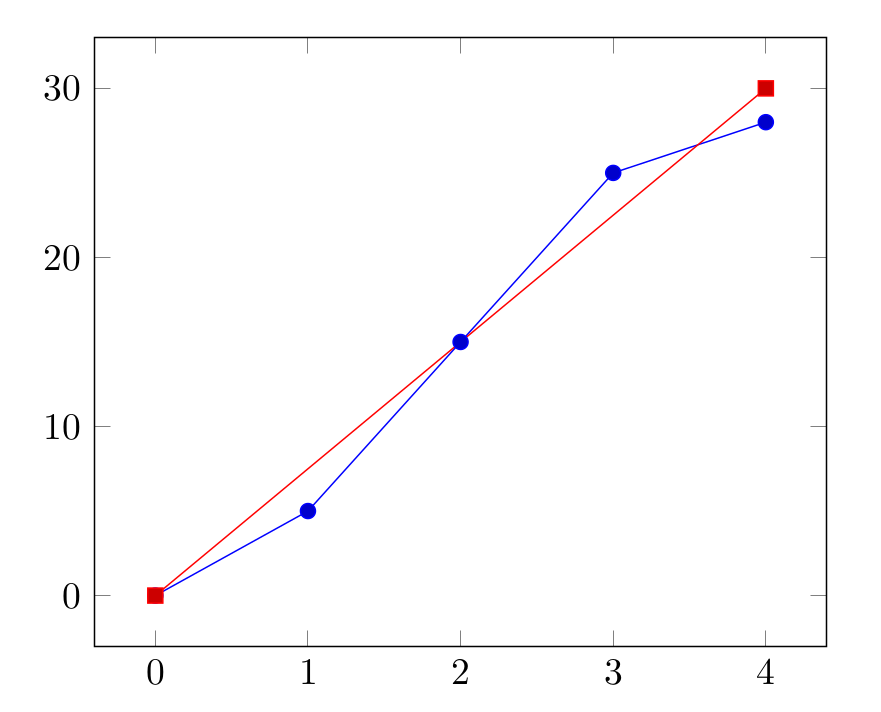
如下圖，紅線是藍線資料的近似線。

插補搜尋法所使用的近似線公式所求出來的索引值功用就如同二元搜尋法的中間索引值，也就是說，若索引值所對應的元素值比要查找的元素值還大的話，下一次搜尋的序列範圍就是此次搜尋的序列範圍的前段(值小的那段)；若索引值所對應的元素值比要查找的元素值還小的話，下一次搜尋的序列範圍就是此次搜尋的序列範圍的後段(值大的那段)。在搜尋不同序列範圍時所使用的近似線公式需重新計算，最簡單取得近似線公式的方式就是利用搜尋範圍中的首、尾兩個點來求出直線公式。

將首點表示為#{{(x_1, y_1)}}#，將尾點表示為#{{(x_2, y_2)}}#，可以求出直線公式為：

#{{{ {y - y_1} = { {y_2 - y_1} \over {x_2 - x_1} } (x - x_1) }}}#

移項之後：

#{{{ x = { {(y - y_1)(x_2 - x_1)} \over {y_2 - y_1} } + x_1 }}}#

以上的#{{x}}#即為要讀取的序列索引值，當然因為算出來不一定是整數，所以需要捨棄小數點或者進位。

插補搜尋法的過程

假設現在有個已排序好的整數陣列，內容如下：

索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81

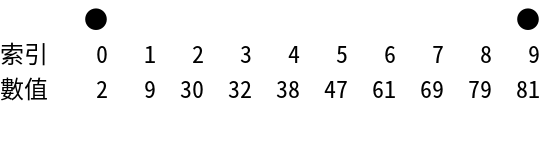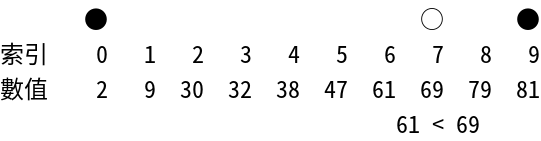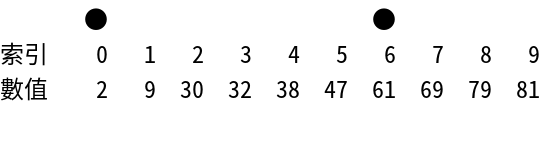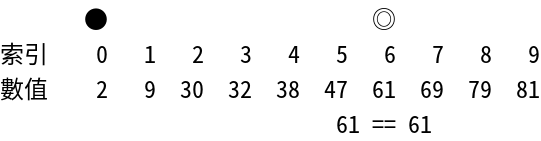
然後我們要用插補搜尋法來找到元素61。

       ●                                  ●
索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81

所以一開始選擇的索引值為：

#{{{ x = { {(61 - 2)(9 - 0)} \over {81 - 2} } + 0 \approx 6.7215 \approx 7 }}}#

       ●                          ○      ●
索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81
                                 61 < 69

       ●                      ●
索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81

接下來選到的索引值為：

#{{{ x = { {(61 - 2)(6 - 0)} \over {61 - 2} } + 0 = 6 }}}#

       ●                      ◎
索引    0   1   2   3   4   5   6   7   8   9
數值    2   9  30  32  38  47  61  69  79  81
                            61 == 61

成功找到元素61在序列中索引6的位置！

插補搜尋法的程式實作

/// 插補搜尋法，使用迴圈來迭代。
pub fn interpolation_search(array: &[i32], target_element: i32) -> Option<usize> {
    let mut start = 0;
    let mut end = array.len() - 1;

    while end >= start {
        let x1 = start as i32;
        let y1 = array[start];
        let x2 = end as i32;
        let y2 = array[end];

        let x = (target_element - y1) * (x2 - x1) / (y2 - y1) + x1;

        if x > x2 || x < x1 {
            break;
        }

        let m = x as usize;

        match target_element.cmp(&array[m]) {
            Ordering::Equal => {
                return Some(m);
            }
            Ordering::Greater => {
                start = m + 1;
            }
            Ordering::Less => {
                if m > 0 {
                    end = m - 1;
                } else {
                    break;
                }
            }
        }
    }

    None
}

/**
 * 插補搜尋法，使用迴圈來迭代。
 */
public static int interpolationSearch(final int[] array, final int targetElement) {
    int start = 0;
    int end = array.length - 1;

    while (end >= start) {
        final int x = (targetElement - array[start]) * (end - start) / (array[end] - array[start]) + start;

        if (x > end || x < start) {
            break;
        }

        if (targetElement == array[x]) {
            return x;
        } else if (targetElement > array[x]) {
            start = x + 1;
        } else {
            end = x - 1;
        }
    }

    return -1;
}

/**
 * 插補搜尋法，使用迴圈來迭代。
 */
function interpolationSearch(array: number[], targetElement: number) {
    let start = 0;
    let end = array.length - 1;

    while (end >= start) {
        const x = Math.floor(((targetElement - array[start]) * (end - start) / (array[end] - array[start])) + start);

        if (x > end || x < start) {
            break;
        }

        if (targetElement === array[x]) {
            return x;
        } else if (targetElement > array[x]) {
            start = x + 1;
        } else {
            end = x - 1;
        }
    }

    return -1;
}

// 插補搜尋法，使用迴圈來迭代。
func InterpolationSearch(array []int, targetElement int) int {
	start := 0
	end := len(array) - 1

	for end >= start {
		x := (targetElement-array[start])*(end-start)/(array[end]-array[start]) + start

		if x > end || x < start {
			break
		}

		if targetElement == array[x] {
			return x
		} else if targetElement > array[x] {
			start = x + 1
		} else {
			end = x - 1
		}
	}

	return -1
}

插補搜尋法的複雜度

以#{{n}}#來表示要搜尋的資料筆數。