動得慢的物體永遠不會被動得快的物體追上？阿基里斯與烏龜的悖論

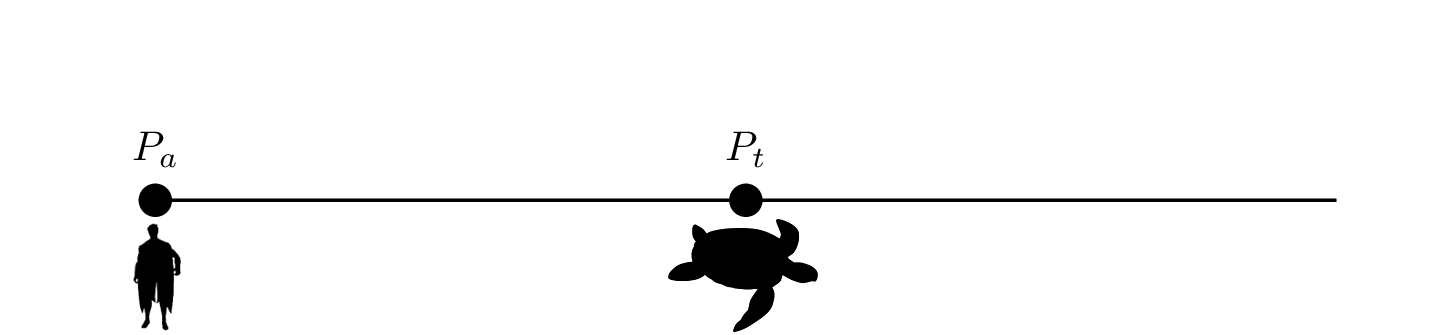
首先我們假設，阿基里斯的所在位置為#{{P_{a}}}#，烏龜的所在位置為#{{P_{t}}}#。示意圖如下：

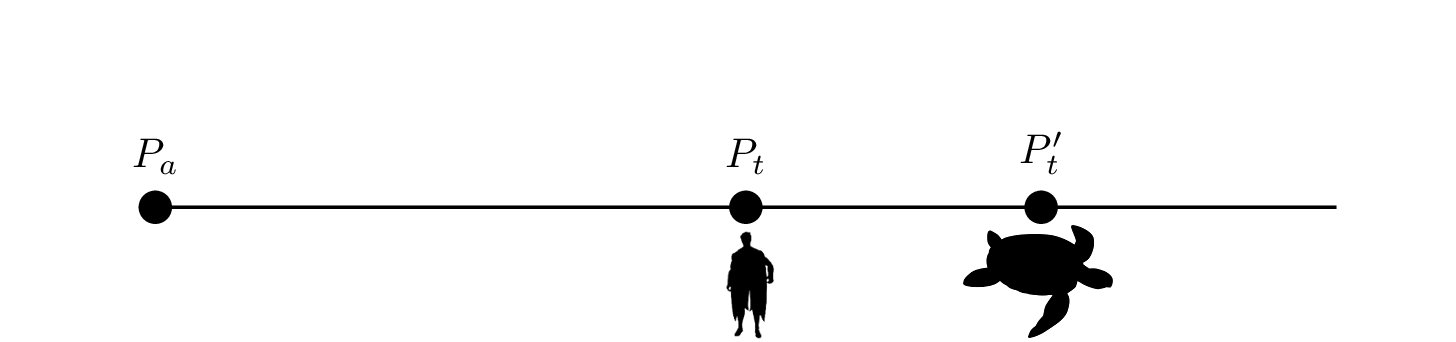
經過#{{t_{1}}}#的時間後，阿基里斯移動到了烏龜原先的#{{P_{t}}}#，這段時間烏龜也朝著同樣的方向移動到了#{{P'_{t}}}#。當然，烏龜的移動速度是比阿基里斯還要慢的，因此烏龜移動的距離#{{P'_{t} - P_{t}}}#，會比阿基里斯移動的距離#{{P_{t} - P_{a}}}#還要來得短。示意圖如下：

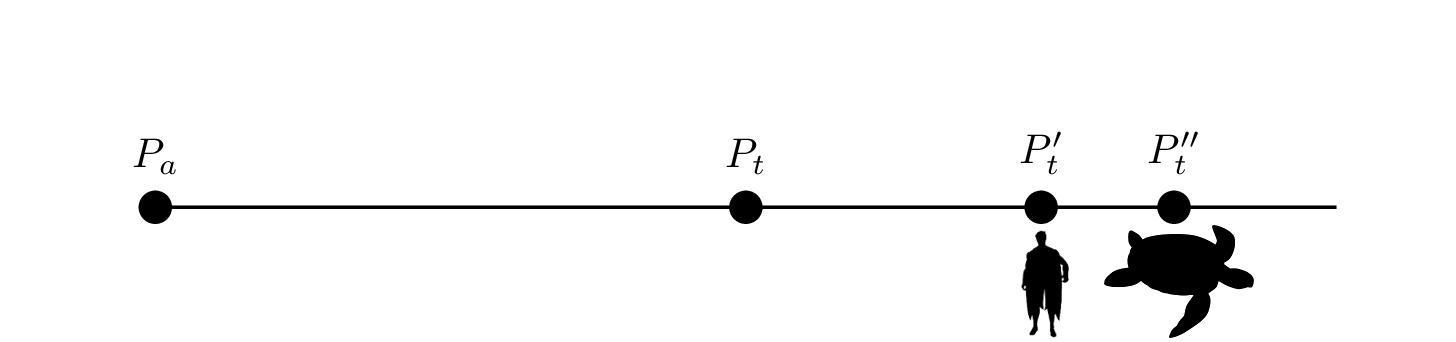
接著又再經過#{{t_{2}}}#的時間，阿基里斯移動到了烏龜原先的#{{P'_{t}}}#，這段時間烏龜也朝著同樣的方向移動到了#{{P''_{t}}}#。示意圖如下：

雖然阿基里斯和烏龜的距離一直有在縮短，但只要阿基里斯往烏龜的所在位置移動，烏龜勢必也會跟著移動到更遠的位置移動。所以我們可以推論阿基里斯根本永遠追不上烏龜！

然而這個推論似乎跟現實有所抵觸，所以到底哪個環節出了問題了呢？

我們不妨假設阿基里斯移動的速度#{{V_{a}}}#是烏龜的速度#{{V_{t}}}#的兩倍，也就是：

#{{{V_{a} = 2V_{t}}}}#

再假設阿基里斯和烏龜最初的距離是#{{L}}#，所以：

#{{{L = P_{t} - P_{a}}}}#

當阿基里斯走到#{{P_{a}}}#時，烏龜也走到#{{P'_{t}}}#了，根據阿基里斯的移動速度是烏龜的兩倍(#{{V_{a} = 2V_{t}}}#)，我們可以再推論出：

#{{{{1 \over 2}L = P'_{t} - P_{t}}}}#

接著當阿基里斯走到#{{P'_{t}}}#時，烏龜也走到#{{P''_{t}}}#了，於是又可以再推論出：

#{{{{1 \over 4}L = P''_{t} - P'_{t}}}}#

如果阿基里斯和烏龜繼續保持速度往同一個方向移動。阿基里斯所走的總路程，可以記為：

#{{{S_{a} = L + {1 \over 2}L + {1 \over 4}L + {1 \over 8}L + {1 \over 16}L + \cdots}}}#

再來看阿基里斯所花的移動時間#{{T_{a}}}#，由於阿基里斯的移動速度是烏龜的兩倍(#{{V_{a} = 2V_{t}}}#)，我們可以推論出：

#{{{t_{2} = {1 \over 2}t_{1}}}}#

設#{{t = t_{1}}}#，則

#{{{T_{a} = t + {1 \over 2}t + {1 \over 4}t + {1 \over 8}t + {1 \over 16}t + \cdots}}}#

從上面的式子我們可以看出什麼呢？因為#{{S_{a}}}#和#{{T_{a}}}#必須不停地加下去，所以表示阿基里斯追烏龜的旅程是沒有終點的嗎？我們先跳出這個框架，想想看另一個新的問題吧！

假設阿基里斯的移動速度是每秒10公尺，而烏龜是每秒5公尺，且一開始烏龜就在阿基里斯前方10公尺處，而阿基里斯則是位在原點。

經過1秒的時間後，阿基里斯移動到10公尺處，烏龜則是移動到15公尺處。再經過1秒的時間，阿基里斯移動到20公尺處，烏龜也是移動到20公尺處。此時阿基里斯就已經追上烏龜了！

誒？等等，那剛才一堆式子到底是在算什麼？事實上，一開始在設想阿基里斯能不能追上或是追過烏龜的這個問題的方式時，方向就已經不太正確了，因為我們一直把「阿基里斯往烏龜在上一個時間點的位置前進」作為推論前提，其實就類似一開始就設定好「阿基里斯(在某時間點之前)永遠落後於烏龜」一樣，與我們要嘗試解答的「阿基里斯能不能追上烏龜」這個問題有矛盾，所以才無法直觀地找出解答。當然，無法直觀地找出解答，並非無解的意思，只是會需要繞一大圈。

#{{S_{a}}}#和#{{T_{a}}}#所代表的涵意其實是：「當阿基里斯非常接近烏龜時，阿基里斯所移動的距離和經過的時間」。以「極限」和「無窮」的概念來看，我們先將#{{S_{a}}}#的式子，利用結合率改寫成：

#{{{
\begin{eqnarray}
S_{a} &=& (2L - {1 \over 2}L) + {1 \over 4}L + {1 \over 8}L + {1 \over 16}L + \cdots \nonumber \\
&=& [(2L - {2 \over 4}L) + {1 \over 4}L] + {1 \over 8}L + {1 \over 16}L + \cdots \nonumber \\
&=& (2L - {1 \over 4}L) + {1 \over 8}L + {1 \over 16}L + \cdots \nonumber \\
&=& [(2L - {2 \over 8}L) + {1 \over 8}L] + {1 \over 16}L + \cdots \nonumber \\
&=& (2L - {1 \over 8}L) + {1 \over 16}L + \cdots \nonumber \\
& & \cdots
\end{eqnarray}
}}}#

#{{T_{a}}}#也可以改寫成：

#{{{
\begin{eqnarray}
T_{a} &=& (2t - {1 \over 8}t) + {1 \over 16}t + \cdots \nonumber \\
& & \cdots
\end{eqnarray}
}}}#

以極限#{{\lim}}#表示的話：

#{{{ S_{a} = \lim_{n \to \infty} (2L - {1 \over 2^n}L) = 2L }}}#

#{{{ T_{a} = \lim_{n \to \infty} (2t - {1 \over 2^n}t) = 2t }}}#

白話一點來說，就是當阿基里斯最接近烏龜(與烏龜的距離無限接近0)時，阿基里斯所移動的距離為一開始和烏龜距離的兩倍，且時間會經過阿基里斯走到烏龜一開始的位置所花的時間的兩倍。換句話說，阿基里斯在持續移動了#{{2t}}#時間之後，就會追過烏龜了。

這個悖論是古希臘哲學家Zeno of Elea(芝諾)所提出的，只能說是一個謬論，因為當時的人們還沒有很清楚地「極限」或是「無窮」的概念，並非都認為#{{ (1 + {1 \over 2} + {1 \over 4} + {1 \over 8} + {1 \over 16} + \cdots) }}#這樣的式子是能解的。

既然剛才是假設阿基里斯的速度是烏龜的兩倍，那麼如果假設阿基里斯的速度是烏龜的十倍呢？

#{{{V_{a} = 10V_{t}}}}#

#{{{
\begin{eqnarray}
S_{a} &=& L + {1 \over 10}L + {1 \over 100}L + {1 \over 1000}L + \cdots \nonumber \\
&=& (1 + {1 \over 10} + {1 \over 100} + {1 \over 1000} + \cdots)L \nonumber \\ \nonumber \\
T_{a} &=& (1 + {1 \over 10} + {1 \over 100} + {1 \over 1000} + \cdots)t
\end{eqnarray}
}}}#

我們可以很明顯地看到此處出現了「等比級數」(#{{1 + {1 \over 10} + {1 \over 100} + {1 \over 1000} + \cdots}}#)，於是我們再根據等比級數公式(首項乘上一減公比的項數次方，再除以一減公比)，可以計算出：

#{{{
\begin{eqnarray}
S_{a} &=& \lim_{n \to \infty} ( { 1 \times { { 1 - ({1 \over 10}) ^ n } \over { 1 - {1 \over 10} } } } L ) \nonumber \\
&=& { { 1 - { \lim\limits_{n \to \infty} {1 \over 10^n} } } \over { 9 \over 10 } } L \nonumber \\
&=& { 10 \over 9 }L \nonumber \\ \nonumber \\
T_{a} &=& { 10 \over 9 }t
\end{eqnarray}
}}}#

便能知道阿基里斯在持續移動了#{{ { 10 \over 9 }t }}#時間或是#{{ { 10 \over 9 }L }}#距離之後，就會追過烏龜了。

事實上，不管是幾倍，只要阿基里斯的速度比烏龜還快，無窮級數就會收斂而有解答。所以，若阿基里斯的移動速度是烏龜移動速度的N倍，且#{{ N > 1 }}#：

#{{{
V_{a} = N \times V_{t}
}}}#

#{{{
\begin{eqnarray}
S_{a} &=& L + {1 \over N}L + {1 \over N^2}L + {1 \over N^3}L + \cdots \nonumber \\
&=& (1 + {1 \over N} + {1 \over N^2} + {1 \over N^3} + \cdots)L \nonumber \\ \nonumber \\
T_{a} &=& t + {1 \over N}t + {1 \over N^2}t + {1 \over N^3}t + \cdots \nonumber \\
&=& (1 + {1 \over N} + {1 \over N^2} + {1 \over N^3} + \cdots)t \nonumber \\
\end{eqnarray}
}}}#

根據等比級數公式：

#{{{
\begin{eqnarray}
& & (1 + {1 \over N} + {1 \over N^2} + {1 \over N^3} + \cdots) \nonumber \\
&=& \lim_{n \to \infty} ( { 1 \times { { 1 - ({1 \over N}) ^ n } \over { 1 - {1 \over N} } } } ) \nonumber \\
&=& { { 1 - { \lim\limits_{n \to \infty} {1 \over N^n} } } \over { {N - 1} \over N } } \nonumber \\
&=& { N \over {N - 1} }
\end{eqnarray}
}}}#

因此：

#{{{
\begin{eqnarray}
S_{a} &=& { N \over {N - 1} }L \nonumber \\ \nonumber \\
T_{a} &=& { N \over {N - 1} }t
\end{eqnarray}
}}}#

完整敘述的話就是，「當烏龜超前阿基里斯#{{L}}#的距離時，若阿基里斯的移動速度#{{V_{a}}}#為烏龜移動速度#{{V_{t}}}#的#{{N}}#倍，則阿基里斯在持續移動了#{{ { N \over {N - 1} }L }}#的距離(或是經過#{{ { N \over {N - 1} } \times {L \over V_{a}} }}#的時間)之後，就會追過烏龜了」。

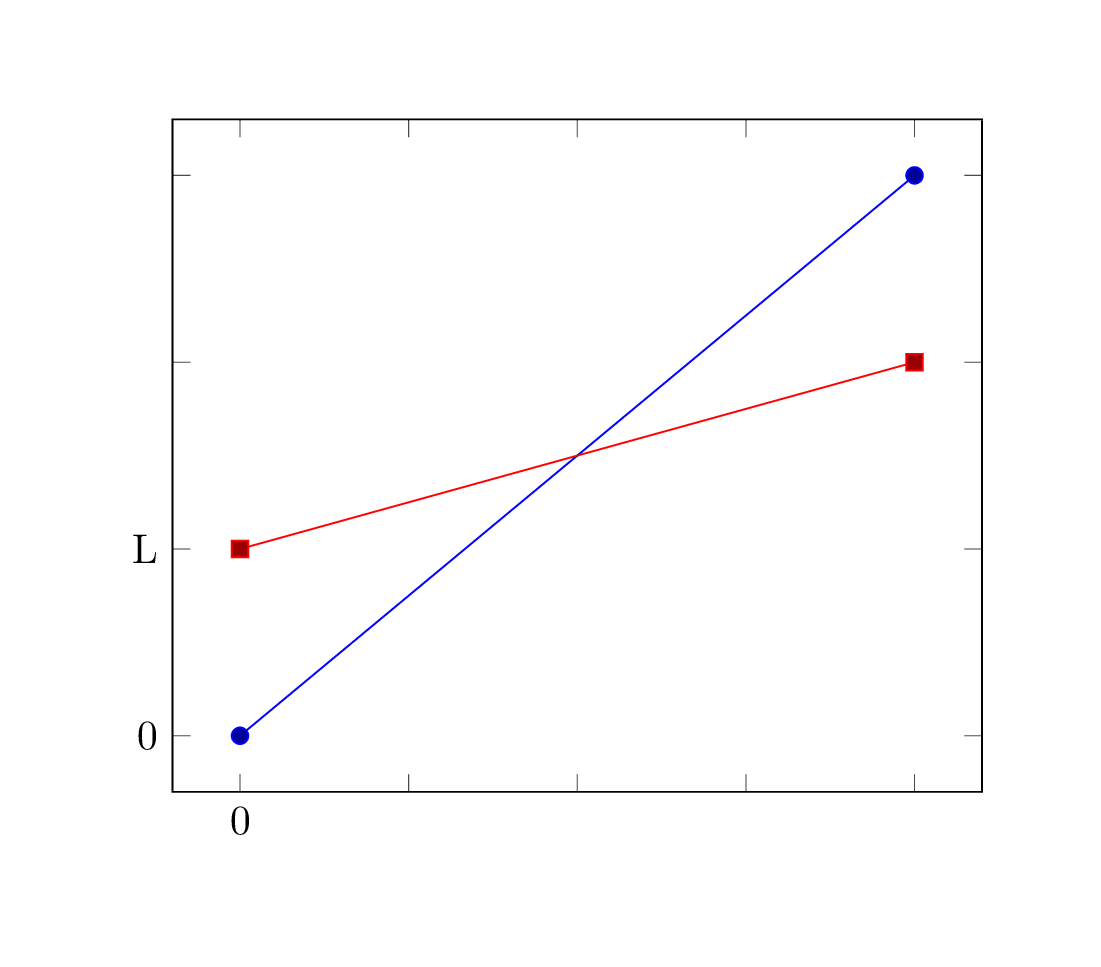
當然，這個問題如果不陷入前提受限的情況，而是直接使用二元一次方程式來說明的話就會非常容易。假設X軸為經過的時間，Y軸為阿基里斯或烏龜所在的位置，而原點#{{ (0, 0) }}#是阿基里斯一開始所在的位置，#{{ (0, L) }}#是烏龜一開始所在的位置。示意圖如下：

在座標軸上畫出來的兩條線的交點便是阿基里斯追上烏龜的時間點和位置。我們可以分別寫出阿基里斯的直線方程式和烏龜的直線方程式：

#{{{
L_{a}: y = a_{1}x
}}}#

#{{{
L_{t}: y = a_{2}x + L
}}}#

若阿基里斯的移動速度為烏龜移動速度的N倍，且#{{ N > 1 }}#，則：

#{{{
{a_{2} \over a_{1}} = {1 \over N}
}}}#

#{{{
a_{2} = {a_{1} \over N}
}}}#

接著求出二元一次方程式的解：

#{{{
\begin{eqnarray}
L_{t} - L_{a}&:& (a_{2} - a_{1})x + L \nonumber \\
&=& ({a_{1} \over N} - a_{1})x + L \nonumber \\
&=& ({{1 - N} \over N})a_{1}x + L \nonumber \\
&=& 0
\end{eqnarray}
}}}#

#{{{
\begin{eqnarray}
a_{1}x &=& -{N \over {1 - N}}L \nonumber \\
&=& -{-N \over {-(1 - N)}}L \nonumber \\
&=& -{-N \over {N - 1}}L \nonumber \\
&=& {N \over {N - 1}}L \nonumber \\ \nonumber \\
y &=& {N \over {N - 1}}L
\end{eqnarray}
}}}#

同樣地可以得出，「當阿基里斯在持續移動了#{{ { N \over {N - 1} }L }}#的距離之後，就會追過烏龜」之結論。