費氏搜尋(Fibonacci Search)演算法，運用費氏數列的搜尋演算法

費氏搜尋(Fibonacci Search)演算法有點像是二元搜尋(Binary Search)演算法，同樣是在一個已排序好的陣列中搜尋元素但是它在移動陣列索引值時是去參考費氏數列(Fibonacci Sequence)，而不是像二元搜尋法那樣總是去取索引的中間值。也由於費氏搜尋法在移動陣列索引值時只需要進行加減運算，不需乘、除法，因此它適合被用在不擅長處理乘、除法的CPU上。

費氏搜尋法(Fibonacci Search)

費氏搜尋法的概念

費氏數列(Fibonacci Sequence)

費氏數列又稱費布那西(Fibonacci)數列，它是一種發散數列，第1項的值為0，第2項的值為1，第#{{n}}#項(#{{ n \geq 3 }}#)的值為第#{{n - 1}}#項和第#{{n - 2}}#項的總和。費氏數列看起來會長得像以下這樣：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

以數學函數#{{F(n)}}#來表示費氏數列的第#{{n}}#項數值，可以寫成：

#{{{
\begin{eqnarray}
F(1) &=& 0 \nonumber \\
F(2) &=& 1 \nonumber \\
F(n) &=& F(n - 1) + F(n - 2), \text{where } n \geq 3 \nonumber \\
\end{eqnarray}
}}}#

不過由於寫程式習慣從0開始數，所以最好還是將費氏數列的第一項設計為#{{F(0)}}#，也就是：

#{{{
\begin{eqnarray}
F(0) &=& 0 \nonumber \\
F(1) &=& 1 \nonumber \\
F(n) &=& F(n - 1) + F(n - 2), \text{where } n \geq 2 \nonumber \\
\end{eqnarray}
}}}#

這篇文章之後都會用#{{F(0)}}#作為費氏數列的第一項。

費氏樹(Fibonacci Tree)與二元搜尋樹(BST, Binary Search Tree)

設一二元樹(Binary Tree)任意節點的數值為整數#{{n}}#，且#{{n > 0}}#。若#{{n > 1}}#，則其左邊子節點的數值為#{{n - 1}}#，右邊子節點的數值為#{{n - 2}}#；若#{{n = 1}}#，則該節點沒有子節點。

所以這個二元樹長出來的結果會像下面這個樣子：

             5
            / \
           /   \
          /     \
         /       \
        /         \
       4           3
      / \         / \
     /   \       /   \
    3     2     2     1
   / \   /     /
  2   1 1     1
 /
1

如果我們利用這個二元樹的節點值去取得費氏數列中對應第幾項的數值，取代原先的節點值。會得到如下的二元樹：

             5
            / \
           /   \
          /     \
         /       \
        /         \
       3           2
      / \         / \
     /   \       /   \
    2     1     1     1
   / \   /     /
  1   1 1     1
 /
1

這個就是費氏樹啦！透過上面畫出的費氏樹，不難發現，根節點為#{{F(5)}}#的費氏樹，其根節點左邊的子樹，就是根節點為#{{F(4)}}#的費氏樹；而根節點為#{{F(5)}}#的費氏樹，其根節點右邊的子樹，就是根節點為#{{F(3)}}#的費氏樹。換句話說，根節點為#{{F(n)}}#的費氏樹，其根節點左邊的子樹，就是根節點為#{{F(n - 1)}}#的費氏樹；而根節點為#{{F(n)}}#的費氏樹，其根節點右邊的子樹，就是根節點為#{{F(n - 2)}}#的費氏樹。

費氏樹其實也就是費氏數列的二元遞迴(Binary Recursion)函數的遞迴樹(Recursion Tree)。

題外話，設#{{S(n)}}#為根節點為#{{F(n)}}#的費氏樹的節點數量，則#{{S(n) = S(n - 1) + S(n - 2) + 1}}#，且#{{S(1) = 1}}#、#{{S(2) = 2}}#。有沒有覺得這東西很像是費氏數列？還真的可以用費氏數列來換算如下(不曉得怎麼算出來的，但是可以由等等會介紹的二元搜尋樹推出來)：

#{{{
S(n) = F(n + 2) - 1
}}}#

那費氏樹和費氏搜尋法有什麼關聯嗎？

我們可以保留費氏樹的節點關係(節點的位置)，先不看節點值，將它當作是一個二元搜尋樹。

二元搜尋樹是一種二元樹。節點如果有左邊子節點的話，其左邊子節點連接的所有值都必須要小於該節點的值；節點如果有右邊子節點的話，其右邊子節點連接的所有值都必須要大於或等於該節點的值。例如以下結構即為二元搜尋樹：

        7
       / \
      /   \
     /     \
    /       \
   3         9
  / \       / \
 /   \     /   \
1     5   8     9
 \   / \
  2 4   6

利用從費氏樹上保留下來的節點關係，從0開始逐次加1，按照二元搜尋樹的規則覆寫費氏樹的所有節點值，會得到如下的二元搜尋樹：

             7
            / \
           /   \
          /     \
         /       \
        /         \
       4          10
      / \         / \
     /   \       /   \
    2     6     9    11
   / \   /     /
  1   3 5     8
 /
0

有沒有發現？以上的二元搜尋樹任意節點與其左、右子節點的差之絕對值都是一樣的。從根節點7開始看的話，會發現一直往左(逐漸變小)的差是#{{F(4)}}#、#{{F(3)}}#、#{{F(2)}}#、#{{F(1)}}#、#{{F(0)}}#(無子節點)這樣變化的(費氏數列的項數每次減1)；而一直往右(逐漸變大)的話會發現差是#{{F(4)}}#、#{{F(2)}}#、#{{F(0)}}#(無子節點)這樣變化的(費氏數列的項數每次減2)。所以，若這一次移動時是往左，則下一次移動時，費氏數列的項數就要先減1；若這一次移動時是往右，則下一次移動時，費氏數列的項數就要先減2。注意這邊的先後順序，並不是比較完大小之後，就去依照往左或往右來看要費氏數列的項數是要減1還是減2來移動索引值。來做個錯誤示範，比如說要走到6好了，若費氏數列的項數初始化為5，7到6要先往左，把費氏數列的項數減1，計算出下一次的索引值是4(#{{7 - F(5 - 1) = 7 - 3 = 4}}#)，接著4到6要先往右，把費氏數列的項數減2，計算出下一次的索引值是5(#{{4 + F(4 - 2) = 4 + 1 = 5}}#)……這樣就錯了！下一次的索引值應為6才對。

用這樣的方式產生的二元搜尋樹其實就是費氏搜尋法分治(Divide)陣列索引值的方式。(如果您不太懂這句的意思，可以先看下一小節以二元搜尋法舉的例子)

假如要排序的陣列a長度是12，其分治方式就正好是上面這棵樹！一開始先去看a[7]，如果要找的元素比a[7]大，下一次就去看a[10]；如果要找的元素比a[7]小，下一次就去看a[4]，依此類推。當遇到#{{F(0)}}#的時候，如果還沒有找到要找的元素，就表示該元素不在這個陣列中。

那麼問題就來了，我們要如何用程式產生出這棵二元搜尋樹？當然，我們其實只需要知道這棵二元搜尋樹的根節點，以及根節點與其子節點的差是費氏數列的第幾項就夠了，因為剩下的可以利用費氏數列從根節點去算。

仔細觀察二元搜尋樹各層最左邊的節點，其實它們就是費氏數列(於最底層從#{{F(2)}}#開始)，只不過被減1了！也就是說，我們其實可以直接藉由陣列的長度(節點的數量)，來產生這棵二元搜尋樹。

繼續以長度為12的陣列為例，由於我們知道某個費氏數列的值(再減1)會剛好就是二元搜尋樹的根節點，且也知道根節點的右子樹它必定不會再包含其它的費氏數列的值(再減1)。因此，利用長度12去尋找在費氏數列中，等於或是小於12的最大費氏數。該數(再減1)就會是二元搜尋樹的根節點值，該數的項數再減2就是根節點與其子節點的差是費氏數列的第幾項。

那如果陣列的長度不是12，而是9呢？按照上面的方式來建二元搜尋樹，根本就是會建出與陣列長度為12時一模一樣的東西嘛！那些「不存在」的索引要怎麼辦？……遇到不存在的索引(超出陣列範圍的索引值)時，直接往左子樹移動即可。

(很多網站提供的費氏搜尋法的演算法和程式碼很古怪，不曉得在算什麼，應該要按照上述的方式來算才是有意義的。)

二元搜尋法的二元搜尋樹與時間複雜度

再補充一下上面提到的二元搜尋樹究竟是什麼用途。如果您還不了解二元搜尋法的話，請先參考這篇文章：

https://magiclen.org/binary-search/

若長度為13的陣列a要用二元搜尋法來搜尋元素的的話，因為是二元搜尋法，所以一開始會先取中間的索引值，也就是6，來看a[6]是不是要找的元素，如果要找的元素比較大，就去看陣列的右半段。右半段也是要先切半，右半段中間的索引值會是9，看a[9]是不是要找的元素……就這樣依此類推，把每次切半所得到的陣列索引值記下來，畫成二元搜尋樹，就是以下的樣子：

           6
          / \
         /   \
        /     \
       /       \
      /         \
     /           \
    2             9
   / \           / \
  /   \         /   \
 /     \       /     \
0       4     7      11
 \     / \     \     / \
  1   3   5     8  10  12

二元搜尋樹的每一層代表進行一次的元素比較，所以二元搜尋法元素最高的比較次數為如上的二元搜尋樹的層數，這也就是為什麼它的最差時間複雜度為#{{ O({\log_{(2)}n}) }}#了。

而既然費氏搜尋法也畫得出類似的二元搜尋樹，我們就知道它的時間複雜度其實也跟二元搜尋樹差不多(忽略產生費氏數列的複雜度)。

題外話，二元搜尋法的二元搜尋樹任意節點之左右子樹的節點數量之比為1:1，而費氏樹的平均比為黃金比例1.618:1。當然，對於在已排序好的陣列中搜尋元素的應用來說，還是二元搜尋法切割的比例更為合理。對比二元搜尋法，費氏搜尋法的優勢僅在於它只需要加減運算。

費氏搜尋法的過程

假設現在有個已排序好的整數陣列，內容如下：

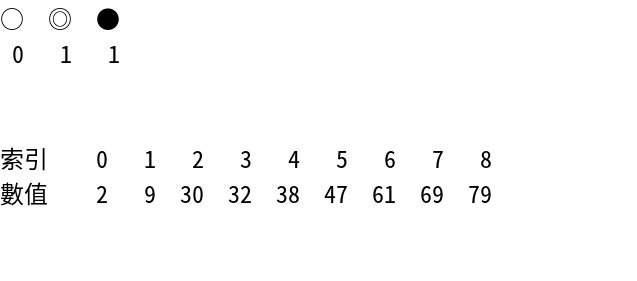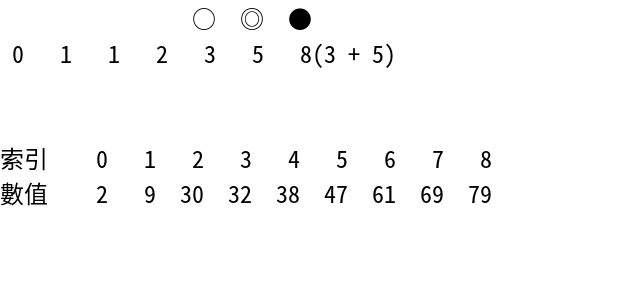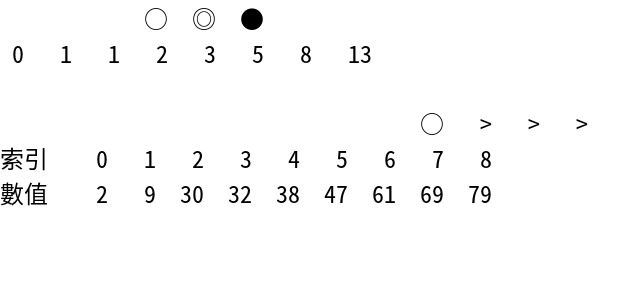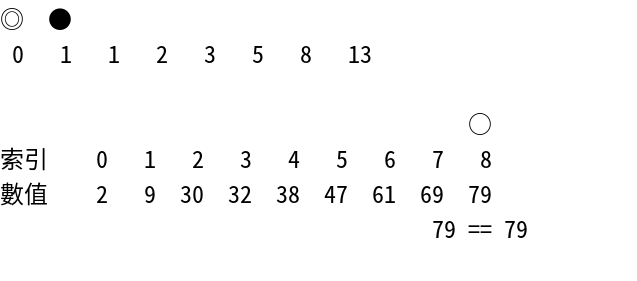
索引    0   1   2   3   4   5   6   7   8
數值    2   9  30  32  38  47  61  69  79

然後我們要用費氏搜尋法來找到元素79。

首先，利用陣列的長度來找出二元搜尋樹的根節點。這個陣列的長度是9，因此在費氏數列中尋找到最大但小於或等於9的費氏數吧！

若已經有這個「費氏數列」，那就只要做單純的搜尋並找出項數就好了。若還沒有這個「費氏數列」，那就要產生出來，產生的過程如下：

○  ◎  ●
 0   1   1

○  ◎  ●
 0   1   1
      9 >= 1

    ○  ◎  ●
 0   1   1   2(1 + 1)


    ○  ◎  ●
 0   1   1   2
          9 >= 2

        ○  ◎  ●
 0   1   1   2   3(1 + 2)


        ○  ◎  ●
 0   1   1   2   3
              9 >= 3

            ○  ◎  ●
 0   1   1   2   3   5(2 + 3)


            ○  ◎  ●
 0   1   1   2   3   5
                  9 >= 5

                ○  ◎  ●
 0   1   1   2   3   5   8(3 + 5)


                ○  ◎  ●
 0   1   1   2   3   5   8
                      9 >= 8

                    ○  ◎   ●
 0   1   1   2   3   5   8   13(5 + 8)


                    ○  ◎   ●
 0   1   1   2   3   5   8   13
                           9 < 13

                    ○  ◎   ●
 0   1   1   2   3   5   8   13

根據以上的過程，我們找出了8這個在費氏數列中最大但小於或等於9的費氏數，同時也找出了8的前一項5和下一項13。

有了費氏數列的連續三項，之後就可以輕易地算出這連續三項前、後的數值。(在費氏搜尋法中只需要用到之前的項)

接著就要開始按照費氏搜尋法之二元搜尋樹的路徑來進行元素比較，並且移動索引值。

首先，先計算比較後，陣列索引要往右或往左移動的距離。根據前面介紹的概念，這個距離會是「費氏數列中最大但小於或等於長度的費氏數」再往前2項的費氏數。所以要利用剛才找到的連續三項費氏數列來推算往前兩項的結果，如下：

             <   <  ○  ◎   ●
 0   1   1   2   3   5   8   13

            ○  ◎  ●
 0   1   1   2   3   5   8   13

可知之後陣列索引應該要往右或往左移動3個距離。

那麼就開始進行比較吧！

             7
               












                                   ○
索引    0   1   2   3   4   5   6   7   8
數值    2   9  30  32  38  47  61  69  79
                                 79 > 69

由於我們要找的元素79比索引7的元素值69還要來得大，所以下一次搜尋所用的索引值是根節點右邊子節點的索引值，也就是7 + 3 = 10。

然後計算之後陣列索引要往右或往左移動的距離。根據前面介紹的概念，由於這次的比較是往右，這個距離會是目前費氏數再往前2項的費氏數。所以要利用已知的連續三項費氏數列來推算往前兩項的結果，如下：

     <   <  ○  ◎  ●
 0   1   1   2   3   5   8   13

    ○  ◎  ●
 0   1   1   2   3   5   8   13

可知之後陣列索引應該要往右或往左移動1個距離。

那麼就開始進行比較吧！由於比較時要看的索引值是10，超出陣列範圍了。

             7
              \
               \
                \
                 \
                  \
                  10
                     






                                               ○
索引    0   1   2   3   4   5   6   7   8
數值    2   9  30  32  38  47  61  69  79

所以直接計算左邊子節點的值，也就是10 - 1 = 9。

然後計算之後陣列索引要往右或往左移動的距離。根據前面介紹的概念，由於這次是往左，這個距離會是目前費氏數再往前1項的費氏數。所以要利用已知的連續三項費氏數列來推算往前兩項的結果，如下：

 <  ○  ◎  ●
 0   1   1   2   3   5   8   13

○  ◎  ●
 0   1   1   2   3   5   8   13

可知之後陣列索引應該要往右或往左移動1個距離。

那麼就開始進行比較吧！由於比較時要看的索引值是9，超出陣列範圍了。

             7
              \
               \
                \
                 \
                  \
                  10
                  /  
                 /    
                9     
                
               


                                           ○
索引    0   1   2   3   4   5   6   7   8
數值    2   9  30  32  38  47  61  69  79

所以直接計算左邊子節點的值，也就是9 - 1 = 8。

○  ◎  ●
 0   1   1   2   3   5   8   13

◎  ●
 0   1   1   2   3   5   8   13

可知之後陣列索引應該要往右或往左移動0個距離。換句話說，若下次比較時還是無法找到要找的元素，該元素就不在這個陣列中。

那麼就開始進行比較吧！比較時要看的索引值是8，如下：

             7
              \
               \
                \
                 \
                  \
                  10
                  /  
                 /    
                9     
               /
              8


                                       ○
索引    0   1   2   3   4   5   6   7   8
數值    2   9  30  32  38  47  61  69  79
                                    79 == 79

如此一來就找到元素79了，其存在於陣列中的索引8的位置。如何？挺快的吧！

費氏搜尋法的程式實作

/// 費氏搜尋法。
pub fn fibonacci_search(array: &[i32], target_element: i32) -> Option<usize> {
    let length = array.len();

    if length == 0 {
        None
    } else {
        let mut previous_fib = 0;
        let mut fib = 1;
        let mut next_fib = 1;

        while next_fib <= length {
            // >> 1
            previous_fib = fib;
            fib = next_fib;
            next_fib += previous_fib; // next_fib = previous_fib + fib
        }

        let mut i = fib - 1;

        // << 2
        next_fib = previous_fib;
        fib -= previous_fib;
        previous_fib = next_fib - fib;

        loop {
            match target_element.cmp(&array[i]) {
                Ordering::Equal => return Some(i),
                Ordering::Less => {
                    if fib == 0 {
                        return None;
                    } else {
                        i -= fib;
                    }

                    // << 1
                    next_fib = fib;
                    fib = previous_fib;
                    previous_fib = next_fib - fib;
                }
                Ordering::Greater => {
                    if fib == 0 {
                        return None;
                    } else {
                        i += fib;
                    }

                    // << 2
                    if previous_fib == 0 {
                        return None;
                    }
                    next_fib = previous_fib;
                    fib -= previous_fib;
                    previous_fib = next_fib - fib;

                    while i >= length {
                        if fib == 0 {
                            return None;
                        } else {
                            i -= fib;
                        }

                        // << 1
                        next_fib = fib;
                        fib = previous_fib;
                        previous_fib = next_fib - fib;
                    }
                }
            }
        }
    }
}

/**
 * 費氏搜尋法。
 */
public static int fibonacciSearch(final int[] array, final int targetElement) {
    final int length = array.length;

    if (length == 0) {
        return -1;
    }

    int previous_fib = 0;
    int fib = 1;
    int next_fib = 1;

    while (next_fib <= length) {
        // >> 1
        previous_fib = fib;
        fib = next_fib;
        next_fib += previous_fib; // next_fib = previous_fib + fib
    }

    int i = fib - 1;

    // << 2
    next_fib = previous_fib;
    fib -= previous_fib;
    previous_fib = next_fib - fib;

    while (true) {
        if (targetElement == array[i]) {
            return i;
        } else if (targetElement < array[i]) {
            if (fib == 0) {
                return -1;
            } else {
                i -= fib;
            }

            // << 1
            next_fib = fib;
            fib = previous_fib;
            previous_fib = next_fib - fib;
        } else {
            if (fib == 0) {
                return -1;
            } else {
                i += fib;
            }

            // << 2
            if (previous_fib == 0) {
                return -1;
            }
            next_fib = previous_fib;
            fib -= previous_fib;
            previous_fib = next_fib - fib;

            while (i >= length) {
                if (fib == 0) {
                    return -1;
                } else {
                    i -= fib;
                }

                // << 1
                next_fib = fib;
                fib = previous_fib;
                previous_fib = next_fib - fib;
            }
        }
    }
}

/**
 * 費氏搜尋法。
 */
function fibonacciSearch(array: number[], targetElement: number) {
    const length = array.length;

    if (length === 0) {
        return -1;
    }

    let previousFib = 0;
    let fib = 1;
    let nextFib = 1;

    while (nextFib <= length) {
        // >> 1
        previousFib = fib;
        fib = nextFib;
        nextFib += previousFib; // nextFib = previousFib + fib
    }

    let i = fib - 1;

    // << 2
    nextFib = previousFib;
    fib -= previousFib;
    previousFib = nextFib - fib;

    for (; ;) {
        if (targetElement === array[i]) {
            return i;
        } else if (targetElement < array[i]) {
            if (fib === 0) {
                return -1;
            } else {
                i -= fib;
            }

            // << 1
            nextFib = fib;
            fib = previousFib;
            previousFib = nextFib - fib;
        } else {
            if (fib === 0) {
                return -1;
            } else {
                i += fib;
            }

            // << 2
            if (previousFib === 0) {
                return -1;
            }
            nextFib = previousFib;
            fib -= previousFib;
            previousFib = nextFib - fib;

            while (i >= length) {
                if (fib === 0) {
                    return -1;
                } else {
                    i -= fib;
                }

                // << 1
                nextFib = fib;
                fib = previousFib;
                previousFib = nextFib - fib;
            }
        }
    }
}

// 費氏搜尋法。
func FibonacciSearch(array []int, targetElement int) (index int) {
	length := len(array)

	if length == 0 {
		return -1
	}

	previous_fib := 0
	fib := 1
	next_fib := 1

	for next_fib <= length {
		// >> 1
		previous_fib = fib
		fib = next_fib
		next_fib += previous_fib // next_fib = previous_fib + fib
	}

	i := fib - 1

	// << 2
	next_fib = previous_fib
	fib -= previous_fib
	previous_fib = next_fib - fib

	for {
		if targetElement == array[i] {
			return i
		} else if targetElement < array[i] {
			if fib == 0 {
				return -1
			} else {
				i -= fib
			}

			// << 1
			next_fib = fib
			fib = previous_fib
			previous_fib = next_fib - fib
		} else {
			if fib == 0 {
				return -1
			} else {
				i += fib
			}

			// << 2
			if previous_fib == 0 {
				return -1
			}
			next_fib = previous_fib
			fib -= previous_fib
			previous_fib = next_fib - fib

			for i >= length {
				if fib == 0 {
					return -1
				} else {
					i -= fib
				}

				// << 1
				next_fib = fib
				fib = previous_fib
				previous_fib = next_fib - fib
			}
		}
	}
}

費氏搜尋法的複雜度

以#{{n}}#來表示要搜尋的資料筆數。

項目	值	備註
最差時間複雜度	#{{O(\log n)}}#	元素不在序列中且元素大小剛好是某些特定值，或者剛好遇到要搜尋的元素位於特定的序列索引值。忽略產生費氏數列的時間複雜度。
最佳時間複雜度	#{{O(1)}}#	要查找的元素的索引值剛好是費氏數列中最大但小於或等於序列長度的費氏數再減`1`。忽略產生費氏數列的時間複雜度。
平均時間複雜度	#{{O(\log n)}}#	忽略產生費氏數列的時間複雜度。
最差空間複雜度	#{{O(1)}}#	永遠只記錄費氏數列的連續三項。