堆積排序(Heap Sort)演算法，利用完全二元樹來排序的演算法

堆積排序(Heap Sort)演算法是利用完全二元樹(Complete Binary Tree)，也就是堆積(Heap)結構來完成排序的演算法。雖然說要用到堆積結構，看起來好像很複雜似的，但其實這個只要一般的陣列結構(可以直接用要排序的陣列來製作)就能實作出來，而且實作出來的速度保證不會太慢，再怎麼差都會有O(nlogn)的時間複雜度。

堆積排序法(Heap Sort)

堆積排序法的概念

堆積排序有法兩個大步驟，第一個是把要排序的陣列製作成「最小堆積」(Min Heap)或是「最大堆積」(Max Heap)。如果要將陣列遞增排序的話就使用最大堆積；如果要遞減排序的話就使用最小堆積。接下來的步驟就是利用最大堆積和最小堆積來進行排序，方法和建立最大堆積或是最小堆積時是幾乎一樣的。

什麼是完全二元樹？完全二元樹是一種二元樹，它只允許最後一層(最底下那層)的節點數量可以不必填滿(若頂層是第1層，則第n層的最大節點數量為2^n-1)。例如以下結構即為完全二元樹：

     5
   /   \
  1     3
 / \   /
6   2 4

什麼是最小堆積？最小堆積就是上層節點數值必定會小於下層節點數值的完全二元樹。例如以下結構即為最小堆積：

     1
   /   \
  2     5
 / \   /
4   6 3

什麼是最大堆積？最大堆積就是上層節點數值必定會大於下層節點數值的完全二元樹。例如以下結構即為最大堆積：

     6
   /   \
  5     3
 / \   /
4   2 1

陣列可以依照索引順序，由左至右、由上到下表示出一個完全二元樹。例如以上的最大堆積，可以是以下這個陣列：

索引    0   1   2   3   4   5
數值    6   5   3   4   2   1

堆積排序法的過程

假設現在有個陣列資料，內容如下：

索引    0   1   2   3   4   5   6   7   8   9
數值   69  81  30  38   9   2  47  61  32  79

要如何將它遞增排列呢？

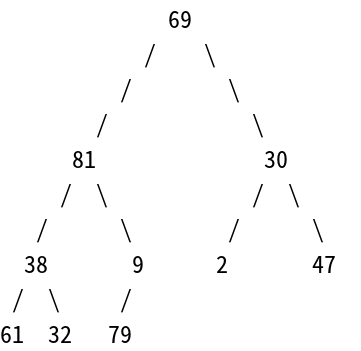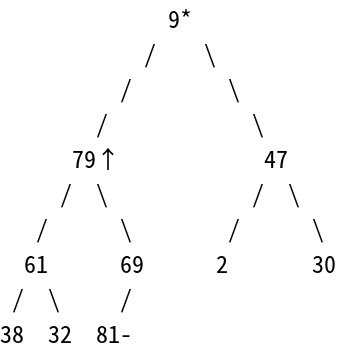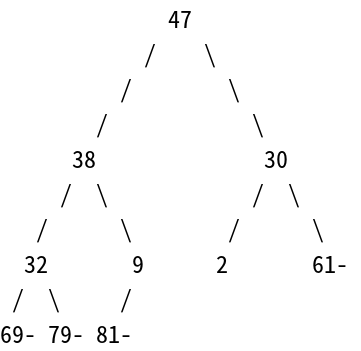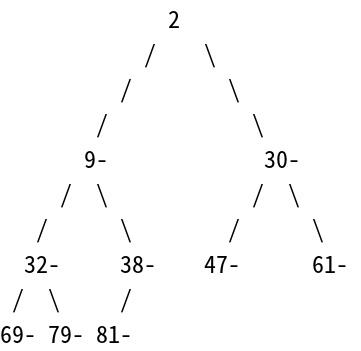
我們先將這個陣列用完全二元樹的結構來表示，如下：

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  38       9      2       47
 /  \     /
61  32   79

由於我們要進行遞增，因此要先將這個完全二元樹變成最大堆積。於是我們從最下面的兩層開始，把比上層大的元素交換到上層。

首先看到47，由於它沒有子節點，因此還不用交換。

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  38       9      2       47*
 /  \     /
61  32   79

2，也沒有子節點，因此不用交換。

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  38       9      2*      47
 /  \     /
61  32   79

再來看到9，9有一個值為79的子節點。由於79比9大，所以要交換上來。

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  38       9*     2       47
 /  \     /
61  32   79↑

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  38      79+     2       47
 /  \     /
61  32   9*

此時9已沒有子節點了，結束交換。

再來看到38，38有兩個子節點，最大的子節點為61。由於61比38大，所以要交換上來。

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  38*     79      2       47
 /  \     /
61↑32   9

              69
            /    \
          /        \
        /            \
      81              30
     /  \            /  \
   /      \        /      \ 
  61+     79      2       47
 /  \     /
38* 32   9

此時38已沒有子節點了，結束交換。

依此類推，剩下的最大堆積的建構過程如下：

              69
            /    \
          /        \
        /            \
      81              30*
     /  \            /  \
   /      \        /      \ 
  61      79      2       47↑
 /  \     /
38  32   9

              69
            /    \
          /        \
        /            \
      81              47+
     /  \            /  \
   /      \        /      \ 
  61      79      2       30*
 /  \     /
38  32   9

              69
            /    \
          /        \
        /            \
      81*             47
     /  \            /  \
   /      \        /      \ 
  61      79      2       30
 /  \     /
38  32   9

              69*
            /    \
          /        \
        /            \
      81↑            47
     /  \            /  \
   /      \        /      \ 
  61      79      2       30
 /  \     /
38  32   9

              81+
            /    \
          /        \
        /            \
      69*             47
     /  \            /  \
   /      \        /      \ 
  61      79↑    2       30
 /  \     /
38  32   9

              81+
            /    \
          /        \
        /            \
      79              47
     /  \            /  \
   /      \        /      \ 
  61      69*     2       30
 /  \     /
38  32   9

              81
            /    \
          /        \
        /            \
      79              47
     /  \            /  \
   /      \        /      \ 
  61      69      2       30
 /  \     /
38  32   9

至此，最大堆積就建立好了！

接下來的工作就是排序啦！由於我們現在已經知道這個結構中的最大值是最頂層的節點，且我們要把陣列做遞增排列。所以我們可以直接把頂層的節點，也就是最大值與陣列的最後一個元素做交換，如此一來我們的遞增排序就已經排好一個元素了。

              9*
            /    \
          /        \
        /            \
      79↑            47
     /  \            /  \
   /      \        /      \ 
  61      69      2       30
 /  \     /
38  32  81-

但別忘了要繼續維持住我們的最大堆積條件，所以還是得做交換才行。由於此時81已經在陣列的正確位置上，我們可以直接把它從最大堆積的考慮範圍中排除，不要再去動它了。

              79+
            /    \
          /        \
        /            \
       9*             47
     /  \            /  \
   /      \        /      \ 
  61      69↑    2       30
 /  \     /
38  32  81-

              79+
            /    \
          /        \
        /            \
      69              47
     /  \            /  \
   /      \        /      \ 
  61       9*     2       30
 /  \     /
38  32  81-

              79
            /    \
          /        \
        /            \
      69              47
     /  \            /  \
   /      \        /      \ 
  61       9      2       30
 /  \     /
38  32  81-

接下來就是讓32要與這個最大堆積結構中的最大值，也就是最頂層的節點做交換啦！之後的步驟都跟剛才把81換下來時一樣，如下：

              32*
            /    \
          /        \
        /            \
      69↑            47
     /  \            /  \
   /      \        /      \ 
  61       9      2       30
 /  \     /
38  79- 81-

              69+
            /    \
          /        \
        /            \
      32*             47
     /  \            /  \
   /      \        /      \ 
  61↑     9      2       30
 /  \     /
38  79- 81-

              69+
            /    \
          /        \
        /            \
      61              47
     /  \            /  \
   /      \        /      \ 
  32*      9      2       30
 /  \     /
38↑79- 81-

              69+
            /    \
          /        \
        /            \
      61              47
     /  \            /  \
   /      \        /      \ 
  38       9      2       30
 /  \     /
32* 79- 81-

              69
            /    \
          /        \
        /            \
      61              47
     /  \            /  \
   /      \        /      \ 
  38       9      2       30
 /  \     /
32  79- 81-

              32*
            /    \
          /        \
        /            \
      61↑            47
     /  \            /  \
   /      \        /      \ 
  38       9      2       30
 /  \     /
69- 79- 81-

              61+
            /    \
          /        \
        /            \
      32*             47
     /  \            /  \
   /      \        /      \ 
  38↑     9      2       30
 /  \     /
69- 79- 81-

              61+
            /    \
          /        \
        /            \
      38              47
     /  \            /  \
   /      \        /      \ 
  32*      9      2       30
 /  \     /
69- 79- 81-

              61
            /    \
          /        \
        /            \
      38              47
     /  \            /  \
   /      \        /      \ 
  32       9      2       30
 /  \     /
69- 79- 81-

              30*
            /    \
          /        \
        /            \
      38              47↑
     /  \            /  \
   /      \        /      \ 
  32       9      2       61-
 /  \     /
69- 79- 81-

              47+
            /    \
          /        \
        /            \
      38              30*
     /  \            /  \
   /      \        /      \ 
  32       9      2       61-
 /  \     /
69- 79- 81-

              47
            /    \
          /        \
        /            \
      38              30
     /  \            /  \
   /      \        /      \ 
  32       9      2       61-
 /  \     /
69- 79- 81-

              2*
            /    \
          /        \
        /            \
      38↑            30
     /  \            /  \
   /      \        /      \ 
  32       9      47-     61-
 /  \     /
69- 79- 81-

              38+
            /    \
          /        \
        /            \
       2*             30
     /  \            /  \
   /      \        /      \ 
  32↑     9      47-     61-
 /  \     /
69- 79- 81-

              38+
            /    \
          /        \
        /            \
      32              30
     /  \            /  \
   /      \        /      \ 
  2*       9      47-     61-
 /  \     /
69- 79- 81-

              38
            /    \
          /        \
        /            \
      32              30
     /  \            /  \
   /      \        /      \ 
  2        9     47-      61-
 /  \     /
69- 79- 81-

              9*
            /    \
          /        \
        /            \
      32↑            30
     /  \            /  \
   /      \        /      \ 
  2       38-    47-      61-
 /  \     /
69- 79- 81-

              32+
            /    \
          /        \
        /            \
       9*             30
     /  \            /  \
   /      \        /      \ 
  2       38-    47-      61-
 /  \     /
69- 79- 81-

              32
            /    \
          /        \
        /            \
       9              30
     /  \            /  \
   /      \        /      \ 
  2       38-    47-      61-
 /  \     /
69- 79- 81-

              2*
            /    \
          /        \
        /            \
       9              30↑
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

              30+
            /    \
          /        \
        /            \
       9              2*
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

              30
            /    \
          /        \
        /            \
       9              2
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

              2*
            /    \
          /        \
        /            \
       9↑            30-
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

              9+
            /    \
          /        \
        /            \
       2*             30-
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

              9
            /    \
          /        \
        /            \
       2              30-
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

              2
            /    \
          /        \
        /            \
       9-             30-
     /  \            /  \
   /      \        /      \ 
  32-     38-    47-      61-
 /  \     /
69- 79- 81-

這樣就完成排序啦！

堆積排序法的程式實作

/// 堆積排序法。
fn heap_sort_inner(array: &mut [i32], shift_down: &dyn Fn(&mut [i32], usize, usize)) {
    let length = array.len();
    let length_dec = length - 1;

    for start in (0..(length >> 1)).rev() {
        shift_down(array, start, length_dec);
    }

    for i in (1..length).rev() {
        array.swap(0, i);
        shift_down(array, 0, i - 1);
    }
}

#[inline]
fn heap_sort_shift_down(array: &mut [i32], mut start: usize, end: usize) {
    loop {
        let left = (start << 1) + 1;

        if left > end {
            break;
        }

        let right = left + 1;

        let max_child = if right <= end && array[right] > array[left] {
            right
        } else {
            left
        };

        if array[start] >= array[max_child] {
            break;
        }

        array.swap(start, max_child);
        start = max_child;
    }
}

#[inline]
fn heap_sort_desc_shift_down(array: &mut [i32], mut start: usize, end: usize) {
    loop {
        let left = (start << 1) + 1;

        if left > end {
            break;
        }

        let right = left + 1;

        let min_child = if right <= end && array[right] < array[left] {
            right
        } else {
            left
        };

        if array[start] <= array[min_child] {
            break;
        }

        array.swap(start, min_child);
        start = min_child;
    }
}

/// 堆積排序法(遞增)。
pub fn heap_sort(array: &mut [i32]) {
    heap_sort_inner(array, &heap_sort_shift_down);
}

/// 堆積排序法(遞增)。
pub fn heap_sort_desc(array: &mut [i32]) {
    heap_sort_inner(array, &heap_sort_desc_shift_down);
}

static abstract class ShiftDown {

    abstract void shiftDown(final int[] array, int start, final int end);
}

static void heapSortInner(final int[] array, final ShiftDown shiftDown) {
    final int length = array.length;
    final int lengthDec = array.length;

    for (int start = (length >> 1) - 1; start >= 0; --start) {
        shiftDown.shiftDown(array, start, lengthDec);
    }

    for (int i = lengthDec; i >= 0; --i) {
        final int temp = array[0];
        array[0] = array[i];
        array[i] = temp;

        shiftDown.shiftDown(array, 0, i - 1);
    }
}

static class AscShiftDown extends ShiftDown {

    @Override
    void shiftDown(final int[] array, int start, final int end) {
        while (true) {
            final int left = (start << 1) + 1;

            if (left > end) {
                break;
            }

            final int right = left + 1;

            final int maxChild = (right <= end && array[right] > array[left]) ? right : left;

            if (array[start] >= array[maxChild]) {
                break;
            }

            final int temp = array[start];
            array[start] = array[maxChild];
            array[maxChild] = temp;

            start = maxChild;
        }
    }
}

static class DescShiftDown extends ShiftDown {

    @Override
    void shiftDown(final int[] array, int start, final int end) {
        while (true) {
            final int left = (start << 1) + 1;

            if (left > end) {
                break;
            }

            final int right = left + 1;

            final int minChild = (right <= end && array[right] < array[left]) ? right : left;

            if (array[start] <= array[minChild]) {
                break;
            }

            final int temp = array[start];
            array[start] = array[minChild];
            array[minChild] = temp;

            start = minChild;
        }
    }
}

/**
 * 堆積排序法(遞增)。
 */
public static void heapSort(final int[] array) {
    heapSortInner(array, new AscShiftDown());
}

/**
 * 堆積排序法(遞減)。
 */
public static void heapSortDesc(final int[] array) {
    heapSortInner(array, new DescShiftDown());
}

/**
 * 堆積排序法。
 */
function heapSortInner(array: number[], shiftDown: (array: number[], start: number, end: number) => void) {
    const length = array.length;
    const lengthDec = length - 1;

    for (let start = (length >> 1) - 1;start >= 0;start--) {
        shiftDown(array, start, lengthDec);
    }

    for (let i = lengthDec;i >= 1;i--) {
        const temp = array[0];
        array[0] = array[i];
        array[i] = temp;

        shiftDown(array, 0, i - 1);
    }
}

function heapSortShiftDown(array: number[], start: number, end: number) {
    for (; ;) {
        const left = (start << 1) + 1;

        if (left > end) {
            break;
        }

        const right = left + 1;

        const maxChild = right <= end && array[right] > array[left] ? right : left;

        if (array[start] >= array[maxChild]) {
            break;
        }

        const temp = array[start];
        array[start] = array[maxChild];
        array[maxChild] = temp;

        start = maxChild;
    }
}

function heapSortDescShiftDown(array: number[], start: number, end: number) {
    for (; ;) {
        const left = (start << 1) + 1;

        if (left > end) {
            break;
        }

        const right = left + 1;

        const minChild = right <= end && array[right] < array[left] ? right : left;

        if (array[start] <= array[minChild]) {
            break;
        }

        const temp = array[start];
        array[start] = array[minChild];
        array[minChild] = temp;

        start = minChild;
    }
}

/**
 * 堆積排序法(遞增)。
 */
function heapSort(array: number[]) {
    heapSortInner(array, heapSortShiftDown);
}

/**
 * 堆積排序法(遞減)。
 */
function heapSortDesc(array: number[]) {
    heapSortInner(array, heapSortDescShiftDown);
}

// 堆積排序法。
func heapSortInner(array []int, shiftDown func([]int, int, int)) {
	length := len(array)
	lengthDec := length - 1

	for start := (length >> 1) - 1; start >= 0; start -= 1 {
		shiftDown(array, start, lengthDec)
	}

	for i := lengthDec; i >= 1; i -= 1 {
		array[0], array[i] = array[i], array[0]
		shiftDown(array, 0, i-1)
	}
}

func heapSortShiftDown(array []int, start int, end int) {
	for {
		left := (start << 1) + 1

		if left > end {
			break
		}

		right := left + 1

		var maxChild int

		if right <= end && array[right] > array[left] {
			maxChild = right
		} else {
			maxChild = left
		}

		if array[start] >= array[maxChild] {
			break
		}

		array[start], array[maxChild] = array[maxChild], array[start]
		start = maxChild
	}
}

func heapSortDescShiftDown(array []int, start int, end int) {
	for {
		left := (start << 1) + 1

		if left > end {
			break
		}

		right := left + 1

		var minChild int

		if right <= end && array[right] < array[left] {
			minChild = right
		} else {
			minChild = left
		}

		if array[start] <= array[minChild] {
			break
		}

		array[start], array[minChild] = array[minChild], array[start]
		start = minChild
	}
}

// 堆積排序法(遞增)。
func HeapSort(array []int) {
	heapSortInner(array, heapSortShiftDown)
}

// 堆積排序法(遞減)。
func HeapSortDesc(array []int) {
	heapSortInner(array, heapSortDescShiftDown)
}

>> 1等同於「除以2取整數」；<< 1等同於「乘以2」。

堆積排序法的複雜度