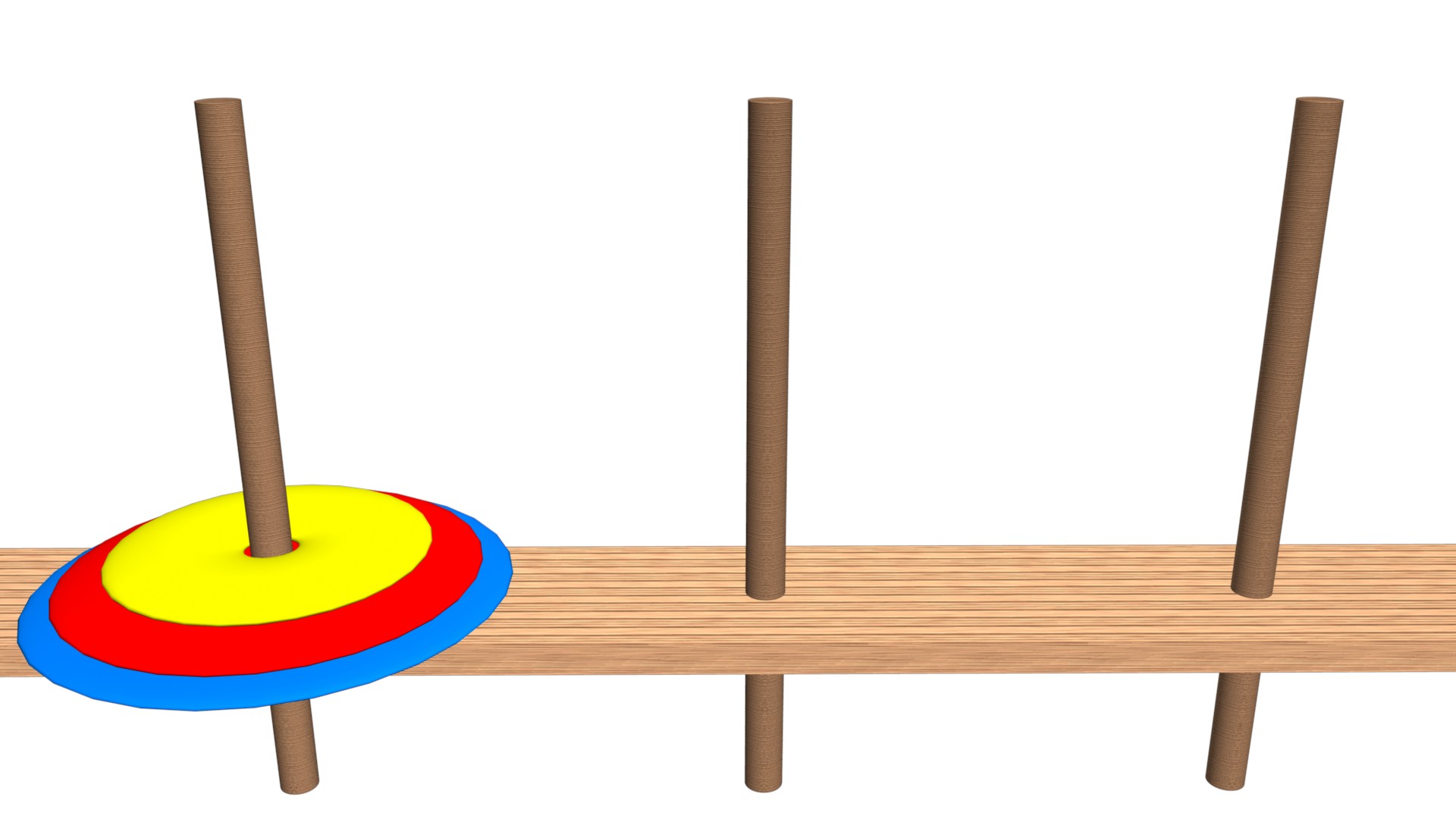
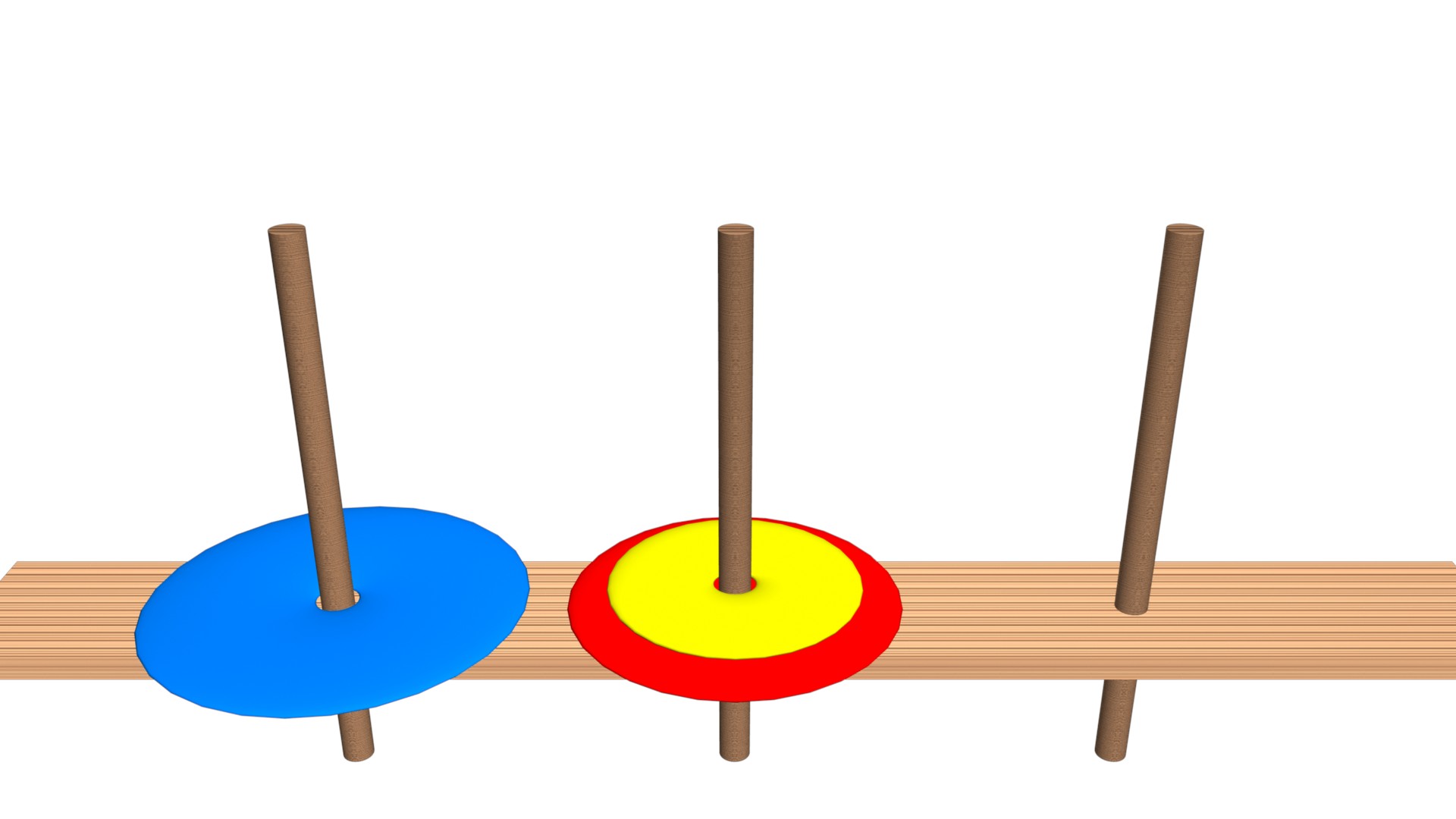
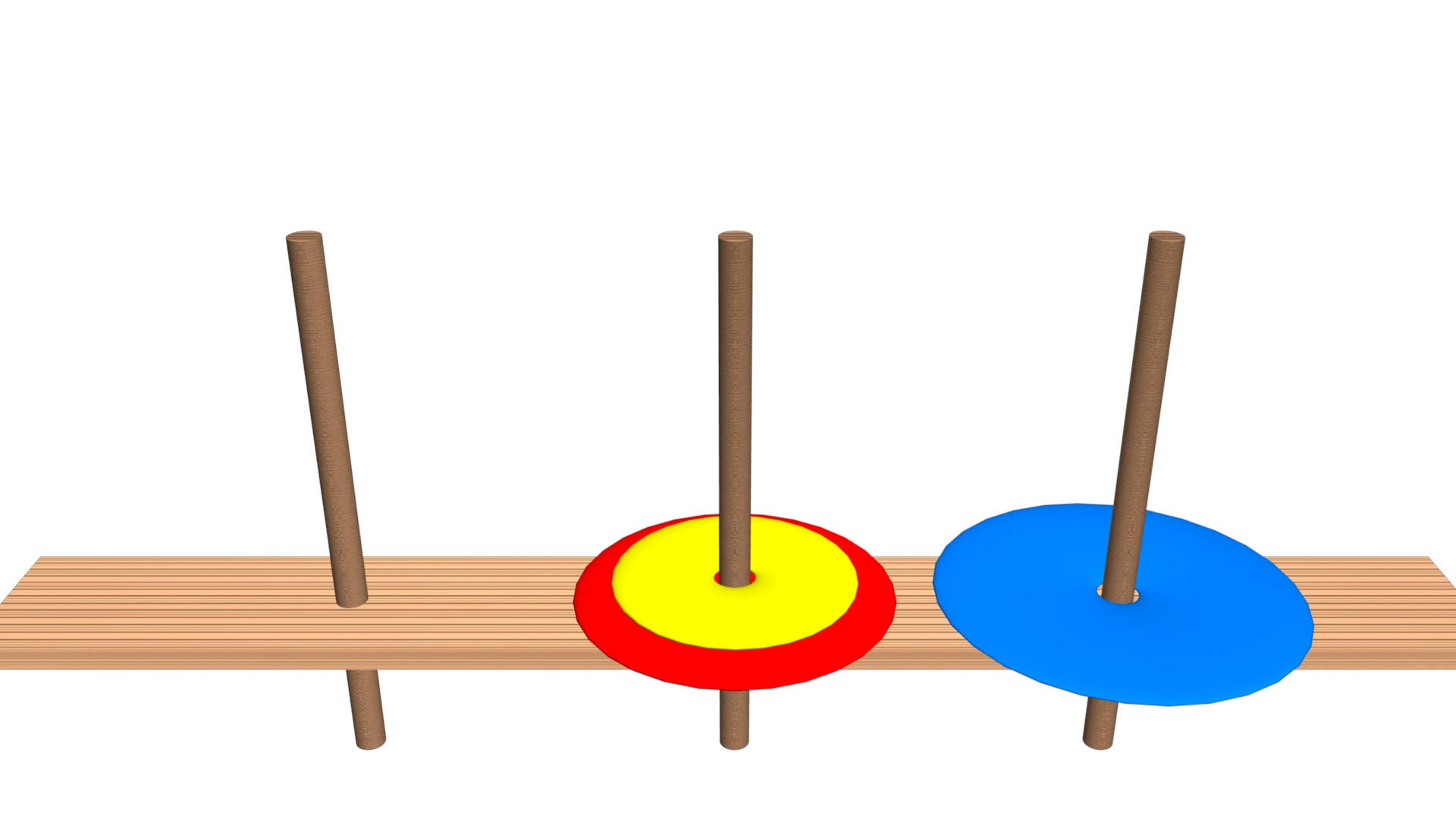
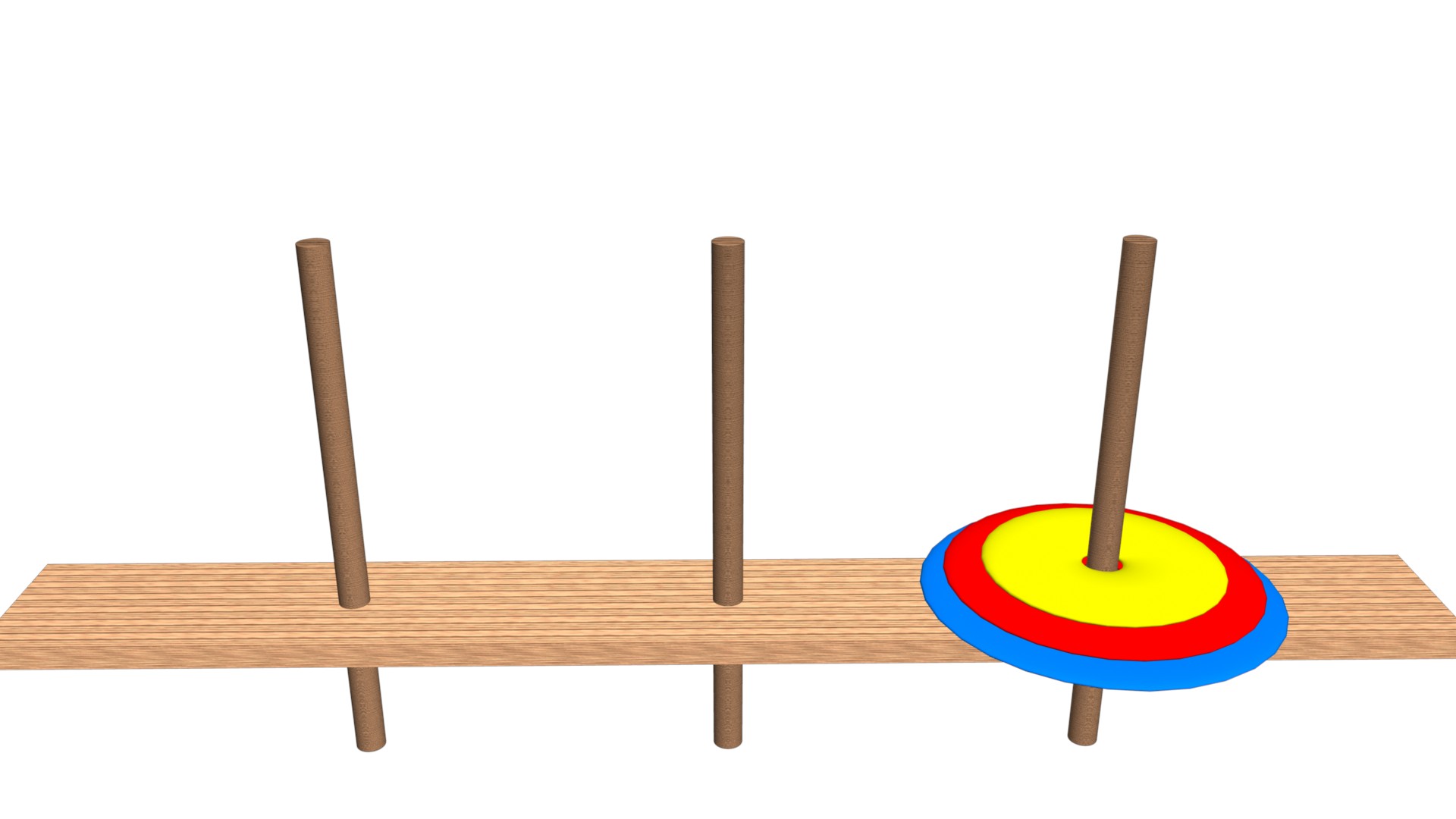
河內塔(Tower of Hanoi)是一個很謎的數學遊戲,它是由三根桿子(Rod)和一個以上大小不同的碟片(Disk)所組成的。在遊戲的一開始,這些碟片按照底大頂小的順序疊在一起,由三根桿子中的其中一根串著。玩家每次可以移動一個碟片到其它的桿子上,但是不能將比較大的碟片疊在比較小的碟片上。當玩家把所有碟片都串到指定的桿子,遊戲就結束了。
如上圖所示,就是一個三碟的河內塔遊戲。習慣上會把最左邊的桿子稱作「A」,是起點。中間的桿子稱作「B」。右邊的桿子稱作「C」,是終點。
所以要完成上面的這個河內塔,就要把左邊的三個碟片移動到右邊。移動方式如下影片:
通常河內塔的遊戲至少會有三個碟片(如果碟片只有兩個以下那還玩個毛),碟片愈多難度愈高。如果您從來沒玩過的話,就算看了上面的影片,應該也還是不知道要怎麼移,或者不知道為什麼要那樣移動。
其實要完成一個河內塔遊戲,碟片的移動方式不只有一種而已。如果我們把影片中的碟片,以黃色、紅色、藍色的順序來表示其所在的桿子,一開始,我們可以用AAA來表示(黃色、紅色、藍色都在A桿子)。下一步,我們只能夠移動黃色碟片到B桿子或是C桿子,所以可以標示為BAA(黃色在B桿子,紅色、藍色在A桿子)或是CAA(黃色在C桿子,紅色、藍色在A桿子)。再下一步,可以移動黃色或紅色碟片到空的桿子上,所以如果這一步是BAA的話,下一步就是BCA或CAA;如果這一步是CAA的話,下一步就是CBA或BAA。
讓我們依此類推,繼續用這樣的標示法來把所有的組合都找出來,會得到如下的結果:
AAA
/ \
BAA-CAA
/ \
BCA CBA
/ \ / \
CCA-ACA-ABA-BBA
/ \
CCB BBC
/ \ / \
ACB-BCB CBC-ABC
/ \ / \
ABB BAB CAC ACC
/ \ / \ / \ / \
BBB-CBB CAB-AAB-AAC-BAC-BCC-CCC
如上,我們把三碟的河內塔所有的移動方式都畫成圖(Graph)了,每條邊所連接的兩個節點表示這兩個節點「只差了一步」。AAA作為我們的起點,CCC作為我們的終點,從上圖可以快速地看出起點到終點的最短路徑為7。換句話說,三碟的河內塔,最少只要移動7步就可以完成。
再仔細看一次上面的影片,可以發現影片中的碟片移動方式正是最短路線。而且我們還可以注意到一個點,那就是我們在把三個碟片移動到C桿子前,有先把兩個碟片移動到B桿子;而在兩個碟片移動到中間前,有先把一個碟片移動到C桿子。也就是說,若我們要移動#{{n}}#個碟片到某指定的桿子上,就要先把#{{n - 1}}#個碟片移動到旁邊的桿子上,此時最大的碟片就可以被移動到指定的桿子上,最後再把旁邊桿子上的#{{n - 1}}#個碟片移來最大的碟片上,#{{n}}#個碟片就都在指定的桿子上啦。
簡而言之,我們找出的「以最短步數解決河內塔問題的演算法」就是:
步驟一:移動A桿子上的#{{n - 1}}#個碟片到B桿子上。
步驟二:移動A桿子剩下的一個碟片到C桿子上。
步驟三:移動B桿子上的所有(#{{n - 1}}#個)碟片到C桿子上。
如何?有沒感覺像是在講屁話?可是電腦真的可以這樣做!
實際寫程式就知道了。首先建立一個hanoi函數,讓它可以透過參數輸入碟片的數量#{{n}}#、起始的桿子、結束的桿子和暫存的桿子。在程式一開始先去判斷碟片的數量是否為1,如果是的話就把碟片從起始的桿子移動到結束的桿子。我們不必真的建立出碟片的物件或是數值,因為河內塔的重點是在找碟片的移動方式。例如:A移到B→A移到C→B移到C。
可以先寫出以下的程式碼:
pub fn hanoi(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
if disk_count == 1 {
println!("Move a disk from {rod_from} to {rod_to}.");
}
}
public static void hanoi(final int disk_count, final char rod_from, final char rod_temp, final char rod_to) {
if (disk_count == 1) {
System.out.printf("Move a disk from %c to %c.%n", rod_from, rod_to);
}
}
function hanoi(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
if (diskCount === 1) {
console.log(`Move a disk from ${rodFrom} to ${rodTo}.`);
}
}
func hanoi(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
if disk_count == 1 {
fmt.Printf("Move a disk from %c to %c.\n", rod_from, rod_to)
}
}
pub fn hanoi(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
if disk_count == 1 {
println!("Move a disk from {rod_from} to {rod_to}.");
} else {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
}
}
public static void hanoi(final int disk_count, final char rod_from, final char rod_temp, final char rod_to) {
if (disk_count == 1) {
System.out.printf("Move a disk from %c to %c.%n", rod_from, rod_to);
} else {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
}
}
function hanoi(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
if (diskCount === 1) {
console.log(`Move a disk from ${rodFrom} to ${rodTo}.`);
} else {
hanoi(diskCount - 1, rodFrom, rodTo, rodTemp);
}
}
func hanoi(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
if disk_count == 1 {
fmt.Printf("Move a disk from %c to %c.\n", rod_from, rod_to)
} else {
hanoi(disk_count-1, rod_from, rod_to, rod_temp)
}
}
接著是步驟二,將起始的桿子上剩下來的一個碟片移動到結束的桿子上。程式碼如下:
pub fn hanoi(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
if disk_count == 1 {
println!("Move a disk from {rod_from} to {rod_to}.");
} else {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
hanoi(1, rod_from, rod_temp, rod_to);
}
}
public static void hanoi(final int disk_count, final char rod_from, final char rod_temp, final char rod_to) {
if (disk_count == 1) {
System.out.printf("Move a disk from %c to %c.%n", rod_from, rod_to);
} else {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
hanoi(1, rod_from, rod_temp, rod_to);
}
}
function hanoi(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
if (diskCount === 1) {
console.log(`Move a disk from ${rodFrom} to ${rodTo}.`);
} else {
hanoi(diskCount - 1, rodFrom, rodTo, rodTemp);
hanoi(1, rodFrom, rodTemp, rodTo);
}
}
func hanoi(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
if disk_count == 1 {
fmt.Printf("Move a disk from %c to %c.\n", rod_from, rod_to)
} else {
hanoi(disk_count-1, rod_from, rod_to, rod_temp)
hanoi(1, rod_from, rod_temp, rod_to)
}
}
最後是步驟三,移動暫存的桿子上所有的,也就是#{{n - 1}}#個碟片到結束的桿子上。程式碼如下:
pub fn hanoi(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
if disk_count == 1 {
println!("Move a disk from {rod_from} to {rod_to}.");
} else {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
hanoi(1, rod_from, rod_temp, rod_to);
hanoi(disk_count - 1, rod_temp, rod_from, rod_to);
}
}
public static void hanoi(final int disk_count, final char rod_from, final char rod_temp, final char rod_to) {
if (disk_count == 1) {
System.out.printf("Move a disk from %c to %c.%n", rod_from, rod_to);
} else {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
hanoi(1, rod_from, rod_temp, rod_to);
hanoi(disk_count - 1, rod_temp, rod_from, rod_to);
}
}
function hanoi(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
if (diskCount === 1) {
console.log(`Move a disk from ${rodFrom} to ${rodTo}.`);
} else {
hanoi(diskCount - 1, rodFrom, rodTo, rodTemp);
hanoi(1, rodFrom, rodTemp, rodTo);
hanoi(diskCount - 1, rodTemp, rodFrom, rodTo);
}
}
func hanoi(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
if disk_count == 1 {
fmt.Printf("Move a disk from %c to %c.\n", rod_from, rod_to)
} else {
hanoi(disk_count-1, rod_from, rod_to, rod_temp)
hanoi(1, rod_from, rod_temp, rod_to)
hanoi(disk_count-1, rod_temp, rod_from, rod_to)
}
}
至此我們就完成遞迴版本的河內塔函數了!很簡單吧!不過筆者當初接觸到河內塔的遞迴函數的時候,根本看不懂它在幹嘛,所以是直接把它背起來,應付考試而已。後來從頭開始釐清河內塔到底在幹什麼,自然就可以寫出遞迴函數了,完全不需要背。
另外我們根據一個碟片的河內塔最少要移動1次來完成、兩個碟片的河內塔最少要移動3次來完成、三個碟片的河內塔最少要移動7次來完成、四個碟片的河內塔最少要移動15次來完成,推測出#{{n}}#個碟片至少需要移動#{{2^n - 1}}#次來完成。利用數學歸納法的證明過程如下。
設#{{S_n}}#為#{{n}}#個碟片最少所需要的移動次數,而根據那三個步驟,我們知道#{{S_{n + 1} = S_n + 1 + S_n}}#。
#{{{
\begin{eqnarray}
\nonumber \\
\text{證明 } S_n &=& 2^n - 1, n \in \mathbb{N^+} \nonumber \\
\nonumber \\
n = 1, \nonumber \\
S_1 &=& 2^1 - 1 = 1 \text{ (成立)} \nonumber \\
\nonumber \\
\text{假設 } n = k, \nonumber \\
S_{k} &=& 2^k - 1 \nonumber \\
\nonumber \\
n = k + 1, \nonumber \\
S_{k + 1} &=& S_k + 1 + S_k \nonumber \\
&=& 2^k - 1 + 1 + 2^k - 1 \nonumber \\
&=& 2^k + 2^k - 1 + 1 - 1 \nonumber \\
&=& 2 \times 2^k - 1 \nonumber \\
&=& 2^{k + 1} - 1 \nonumber \\
\nonumber \\
\therefore S_n &=& 2^n - 1, n \in \mathbb{N^+} \text{ 是正確的}
\end{eqnarray}
}}}#
程式寫出來了,但還是不知道怎麼玩河內塔……
即便理解河內塔主要想展示的思想(大問題分解成小問題,也就是遞迴啦),在現實中使用教具或是桌遊玩具玩河內塔,甚至是玩河內塔的電子遊戲時,碟片數量超過三個的時候還是不知道該如何下手啊!畢竟人腦不像電腦那樣,可以快速以遞迴的方式來思考問題。
所以我們必須要再想個「迭代」的方式來解決河內塔的問題。
在開始想之前,可以先看看下面這篇文章,將遞迴版本的河內塔直接轉成迭代版本。
轉出來的程式如下:
pub fn hanoi(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
let mut stack = Vec::new();
stack.push((disk_count, rod_from, rod_temp, rod_to));
while let Some((disk_count, rod_from, rod_temp, rod_to)) = stack.pop() {
if disk_count == 1 {
println!("Move a disk from {rod_from} to {rod_to}.");
} else {
stack.push((disk_count - 1, rod_temp, rod_from, rod_to));
stack.push((1, rod_from, rod_temp, rod_to));
stack.push((disk_count - 1, rod_from, rod_to, rod_temp));
}
}
}
public static void hanoi(int disk_count, char rod_from, char rod_temp, char rod_to) {
final Stack<Object> stack = new Stack<>();
stack.push(disk_count);
stack.push(rod_from);
stack.push(rod_temp);
stack.push(rod_to);
while (!stack.empty()) {
rod_to = (char) stack.pop();
rod_temp = (char) stack.pop();
rod_from = (char) stack.pop();
disk_count = (int) stack.pop();
if (disk_count == 1) {
System.out.printf("Move a disk from %c to %c.%n", rod_from, rod_to);
} else {
stack.push(disk_count - 1);
stack.push(rod_temp);
stack.push(rod_from);
stack.push(rod_to);
stack.push(1);
stack.push(rod_from);
stack.push(rod_temp);
stack.push(rod_to);
stack.push(disk_count - 1);
stack.push(rod_from);
stack.push(rod_to);
stack.push(rod_temp);
}
}
}
function hanoi(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
const stack: [number, string, string, string][] = [];
stack.push([
diskCount, rodFrom, rodTemp, rodTo,
]);
while (stack.length > 0) {
[
diskCount, rodFrom, rodTemp, rodTo,
// eslint-disable-next-line @typescript-eslint/no-non-null-assertion
] = stack.pop()!;
if (diskCount === 1) {
console.log(`Move a disk from ${rodFrom} to ${rodTo}.`);
} else {
stack.push([
diskCount - 1, rodFrom, rodFrom, rodTo,
]);
stack.push([
1, rodFrom, rodTemp, rodTo,
]);
stack.push([
diskCount - 1, rodFrom, rodTo, rodTemp,
]);
}
}
}
type stack []interface{}
func (s stack) Push(v interface{}) stack {
return append(s, v)
}
func (s stack) PopRune() (stack, rune) {
l := len(s)
return s[:l-1], s[l-1].(rune)
}
func (s stack) PopInt() (stack, int) {
l := len(s)
return s[:l-1], s[l-1].(int)
}
func hanoi(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
stack := make(stack, 0)
stack = stack.Push(disk_count)
stack = stack.Push(rod_from)
stack = stack.Push(rod_temp)
stack = stack.Push(rod_to)
for len(stack) > 0 {
stack, rod_to = stack.PopRune()
stack, rod_temp = stack.PopRune()
stack, rod_from = stack.PopRune()
stack, disk_count = stack.PopInt()
if disk_count == 1 {
fmt.Printf("Move a disk from %c to %c.\n", rod_from, rod_to)
} else {
stack = stack.Push(disk_count - 1)
stack = stack.Push(rod_temp)
stack = stack.Push(rod_from)
stack = stack.Push(rod_to)
stack = stack.Push(1)
stack = stack.Push(rod_from)
stack = stack.Push(rod_temp)
stack = stack.Push(rod_to)
stack = stack.Push(disk_count - 1)
stack = stack.Push(rod_from)
stack = stack.Push(rod_to)
stack = stack.Push(rod_temp)
}
}
}
以上的河內塔函數,雖然已經是迭代版本了沒錯,但骨子裡還是用遞迴(或者更準確來說是Top-down)的方式在算的,看看就好。
其實多玩幾次三個碟片的河內塔和四個碟片的河內塔(或是也可以玩兩個碟片,如果您真的不太會玩河內塔的話),就可以發現如果要用最少的步數來完成河內塔的話,三個碟片和四個碟片分別在一開始,最小的碟片必須要移動往不同的桿子。像是三個碟片的河內塔,第一步就必須要先將最小的碟片從A桿移到C桿;而四個碟片的河內塔,第一步就必須要先將最小的碟片從A桿移到B桿。這是為了要確保#{{n - 1}}#個碟片在移動之後,是在暫存的桿子上,而不是在結束的桿子上,好讓我們能把起始的桿子上的最大的碟片移動到結束的桿子。若#{{n - 1}}#個碟片在移動之後,是在結束的桿子上,那我們也就只能再把#{{n - 1}}#個碟片搬到暫存的桿子上後,才能把起始的桿子上的最大的碟片移動到結束的桿子。
也就是說,河內塔第一步最小的碟片移動的方式,要根據碟片的數量是奇數還是偶數來決定。如果是三個碟片的河內塔,那第一步就是把最小的碟片從A桿移到C桿;如果是四個碟片的河內塔,那第一步就是把最小的碟片從A桿移到B桿。
若您還不了解的話,試想一下,若我們玩四個碟片的河內塔,第一步是把最小的碟片從A桿移到C桿的話,那不就跟在玩三個碟片的河內塔時一樣,就會先把三個碟片移動到C桿了,然後又得把那三個碟片再移到B桿上,才能將A桿上最大的碟片移到C桿,所以這對四個碟片的河內塔遊戲來說也就不會是一個最佳的解決方式。
所以知道第一步要怎麼移之後呢?我們都知道河內塔的碟片只是大的在下、小的在上,因此最小的碟片在被移動之後,勢必得趕緊移回第二小的碟片之上,不然任何其它的碟片都無法使用最小的碟片所在的桿子。當然,我們不會在移動完最小的碟片後,下一步又把它移回去,或者又把它移動到另一個桿子上,因為這樣一點意義都沒有。也就是說,我們合理能做的第二步,就是將第二小的碟片移動到另一個桿子上,然後在第三步的時候,把最小的碟片移到第二小的碟片所在的桿子上。此時就完成了兩個碟片的移動。
再來要進行第四步的時候,我們就會發現,除了將最小的碟片又移動到其它桿子上外,其實也只剩下一種移動方式。在此時若將最小的碟片又移動到其它桿子上,就等同於又要開始進行最小和第二小的碟片的移動,沒有意義。所以我們也只能夠選擇剩下的那一種移動方式。
第五步時,我們不考慮去還原第四步,就只會剩下一種移動方式,那就是花費三步(第五步、第六步、第七步)去移動最小和第二小的碟片。
第八步時,同理,除了將最小的碟片又移動到其它桿子上外,其實也只剩下一種移動方式。
聰明的讀者們大概都看得出來這其中的規律了吧!也就是「四步一循環」:移動最小的碟片→移動第二小的碟片→移動最小的碟片到第二小的碟片上→移動其它的碟片。
現在的問題是在於,「移動最小的碟片」時,該碟片因為最小,所以另外兩個桿子都可以成為目標,但除了第一步我們知道最小的碟片究竟要移動到哪個桿子之外,第五步、第九步……到達這些後續的步數時,就不知道該怎麼移動了。
事實上,如果我們觀察河內塔最短步數的移動方式,會在「移動最小的碟片」的步驟時,發現它們總是往同一個「方向」移動一個距離。以三個碟片的河內塔來說,一開始將最小的碟片從A桿移到C桿,看作是「向左」(A桿子向左會到C桿子,形成循環);而四個碟片的河內塔,一開始將最小的碟片從A桿移到B桿,看作是「向右」(C桿子向右會到A桿子,形成循環)。找出這個「向左」、「向右」規律後,我們可以擴充一下我們剛剛發現的「四步一循環」規則:
- 0. 判斷碟片的數量是奇數還是偶數,來決定最小的碟片和第二小的碟片移動時的方向。偶數往右;奇數往左。
- 1. 移動最小的碟片一個桿子的距離。
- 2. 移動第二小的碟片兩個桿子的距離。
- 3. 移動最小的碟片一個桿子的距離。(將最小的碟片移動到第二小的碟片上。)
- 4. 移動其它的碟片。
如此一來在遊玩河內塔的時候,我們可以在心中默念「一、二、三、四」,按照步驟來解決河內塔,完全不需要動腦。
總算會玩了吧!那用這樣的方式寫程式來實作一個迭代版本的河內塔函數如何?程式如下:
fn move_disk(from: char, to: char) {
println!("Move a disk from {from} to {to}.");
}
pub fn hanoi_iteratively(disk_count: usize, mut rod_from: char, mut rod_temp: char, mut rod_to: char) {
if disk_count & 1 == 1 {
let temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
let end = 2f64.powf(disk_count as f64) as usize - 1;
let mut step = 1;
for _ in 0..end {
match step {
1 => move_disk(rod_from, rod_temp),
2 => move_disk(rod_from, rod_to),
3 => move_disk(rod_temp, rod_to),
_ => {
println!("Move a disk from ? to ?.");
let from = rod_from;
let temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
}
step += 1;
}
}
static void moveDisk(final char from, final char to) {
System.out.printf("Move a disk from %c to %c.%n", from, to);
}
public static void hanoiIteratively(final int disk_count, char rod_from, char rod_temp, char rod_to) {
if ((disk_count & 1) == 1) {
final char temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
final int end = (int) Math.pow(2, disk_count) - 1;
int step = 1;
for (int i = 0; i < end; ++i) {
switch (step) {
case 1:
moveDisk(rod_from, rod_temp);
break;
case 2:
moveDisk(rod_from, rod_to);
break;
case 3:
moveDisk(rod_temp, rod_to);
break;
case 4:
System.out.println("Move a disk from ? to ?.");
final char from = rod_from;
final char temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
++step;
}
}
function moveDisk(from: string, to: string) {
console.log(`Move a disk from ${from} to ${to}.`);
}
function hanoiIteratively(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
if ((diskCount & 1) === 1) {
const temp = rodTemp;
rodTemp = rodTo;
rodTo = temp;
}
const end = (2 ** diskCount) - 1;
let step = 1;
for (let i = 0;i < end;i++) {
switch (step) {
case 1:
moveDisk(rodFrom, rodTemp);
break;
case 2:
moveDisk(rodFrom, rodTo);
break;
case 3:
moveDisk(rodTemp, rodTo);
break;
case 4: {
console.log("Move a disk from ? to ?.");
const from = rodFrom;
const temp = rodTemp;
rodFrom = rodTo;
rodTemp = from;
rodTo = temp;
step = 1;
continue;
}
}
step += 1;
}
}
func moveDisk(from rune, to rune) {
fmt.Printf("Move a disk from %c to %c.\n", from, to)
}
func hanoiIteratively(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
if disk_count&1 == 1 {
temp := rod_temp
rod_temp = rod_to
rod_to = temp
}
end := int(math.Pow(2.0, float64(disk_count))) - 1
step := 1
for i := 0; i < end; i++ {
switch step {
case 1:
moveDisk(rod_from, rod_temp)
case 2:
moveDisk(rod_from, rod_to)
case 3:
moveDisk(rod_temp, rod_to)
case 4:
fmt.Println("Move a disk from ? to ?.")
from := rod_from
temp := rod_temp
rod_from = rod_to
rod_temp = from
rod_to = temp
step = 1
continue
}
step++
}
}
以上程式,將「向左」、「向右」的問題以交換除了起始的桿子之外的兩個桿子來簡化。試想一下,向右的順序如果是ABCABC,那麼向左就是ACBABC,這不就是把B、C兩個桿子交換了嗎?
再來,一個循環的第四步如果我們不知道當下碟片的分佈情形,就不知道要怎麼移動了(以上程式先以Move a disk from ? to ?.來輸出)。所以我們必須在每步都去改變並記錄碟片的分佈情形才行,可以用一個堆疊來模擬一個桿子,三個桿子就是三個堆疊。將以上程式加入堆疊後的樣子如下:
fn move_disk(stacks: &mut [Vec<usize>], rod_names: &[char], from: usize, to: usize) {
let disk = stacks[from].pop().unwrap();
stacks[to].push(disk);
println!("Move a disk from {} to {}.", rod_names[from], rod_names[to]);
}
pub fn hanoi_iteratively(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
let rod_names = [rod_from, rod_temp, rod_to];
let mut stacks = [Vec::new(), Vec::new(), Vec::new()];
let mut rod_from = 0;
let mut rod_temp = 1;
let mut rod_to = 2;
if disk_count & 1 == 1 {
let temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
for stack in stacks.iter_mut() {
stack.push(0);
}
for i in 1..=disk_count {
stacks[rod_from].push(i);
}
let end = 2f64.powf(disk_count as f64) as usize - 1;
let mut step = 1;
for _ in 0..end {
match step {
1 => move_disk(&mut stacks, &rod_names, rod_from, rod_temp),
2 => move_disk(&mut stacks, &rod_names, rod_from, rod_to),
3 => move_disk(&mut stacks, &rod_names, rod_temp, rod_to),
_ => {
println!("Move a disk from ? to ?.");
let from = rod_from;
let temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
}
step += 1;
}
}
static void moveDisk(final Stack<Integer>[] stacks, final char[] rod_names, final int from, final int to) {
final Integer disk = stacks[from].pop();
stacks[to].push(disk);
System.out.printf("Move a disk from %c to %c.%n", rod_names[from], rod_names[to]);
}
public static void hanoiIteratively(final int disk_count, char rod_from_name, char rod_temp_name, char rod_to_name) {
final char[] rod_names = new char[]{rod_from_name, rod_temp_name, rod_to_name};
final Stack<Integer>[] stacks = new Stack[]{new Stack<>(), new Stack<>(), new Stack<>()};
int rod_from = 0;
int rod_temp = 1;
int rod_to = 2;
if ((disk_count & 1) == 1) {
final int temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
for (int i = 0; i < stacks.length; ++i) {
stacks[i].push(0);
}
for (int i = 1; i <= disk_count; ++i) {
stacks[rod_from].push(i);
}
final int end = (int) Math.pow(2, disk_count) - 1;
int step = 1;
for (int i = 0; i < end; ++i) {
switch (step) {
case 1:
moveDisk(stacks, rod_names, rod_from, rod_temp);
break;
case 2:
moveDisk(stacks, rod_names, rod_from, rod_to);
break;
case 3:
moveDisk(stacks, rod_names, rod_temp, rod_to);
break;
case 4:
System.out.println("Move a disk from ? to ?.");
final int from = rod_from;
final int temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
++step;
}
}
function moveDisk(stacks: number[][], rodNames: string[], from: number, to: number) {
// eslint-disable-next-line @typescript-eslint/no-non-null-assertion
const disk = stacks[from].pop()!;
stacks[to].push(disk);
console.log(`Move a disk from ${rodNames[from]} to ${rodNames[to]}.`);
}
function hanoiIteratively(diskCount: number, rodFromName: string, rodTempName: string, rodToName: string) {
const rodNames = [rodFromName, rodTempName, rodToName];
const stacks: number[][] = [[], [], []];
let rodFrom = 0;
let rodTemp = 1;
let rodTo = 2;
if ((diskCount & 1) === 1) {
const temp = rodTemp;
rodTemp = rodTo;
rodTo = temp;
}
for (const stack of stacks) {
stack.push(0);
}
for (let i = 1;i <= diskCount;i++) {
stacks[rodFrom].push(i);
}
const end = (2 ** diskCount) - 1;
let step = 1;
for (let i = 0;i < end;i++) {
switch (step) {
case 1:
moveDisk(stacks, rodNames, rodFrom, rodTemp);
break;
case 2:
moveDisk(stacks, rodNames, rodFrom, rodTo);
break;
case 3:
moveDisk(stacks, rodNames, rodTemp, rodTo);
break;
case 4: {
console.log("Move a disk from ? to ?.");
const from = rodFrom;
const temp = rodTemp;
rodFrom = rodTo;
rodTemp = from;
rodTo = temp;
step = 1;
continue;
}
}
step += 1;
}
}
type stack []int
func (s stack) Push(v int) stack {
return append(s, v)
}
func (s stack) Pop() (stack, int) {
l := len(s)
return s[:l-1], s[l-1]
}
func moveDisk(stacks []stack, rod_names []rune, from int, to int) {
var disk int
stacks[from], disk = stacks[from].Pop()
stacks[to] = stacks[to].Push(disk)
fmt.Printf("Move a disk from %c to %c.\n", rod_names[from], rod_names[to])
}
func hanoiIteratively(disk_count int, rod_from_name rune, rod_temp_name rune, rod_to_name rune) {
rod_names := []rune{rod_from_name, rod_temp_name, rod_to_name}
stacks := []stack{make(stack, 0), make(stack, 0), make(stack, 0)}
rod_from := 0
rod_temp := 1
rod_to := 2
if disk_count&1 == 1 {
temp := rod_temp
rod_temp = rod_to
rod_to = temp
}
for i := 0; i < len(stacks); i++ {
stacks[i] = stacks[i].Push(0)
}
for i := 1; i <= disk_count; i++ {
stacks[rod_from] = stacks[rod_from].Push(i)
}
end := int(math.Pow(2.0, float64(disk_count))) - 1
step := 1
for i := 0; i < end; i++ {
switch step {
case 1:
moveDisk(stacks, rod_names, rod_from, rod_temp)
case 2:
moveDisk(stacks, rod_names, rod_from, rod_to)
case 3:
moveDisk(stacks, rod_names, rod_temp, rod_to)
case 4:
fmt.Println("Move a disk from ? to ?.")
from := rod_from
temp := rod_temp
rod_from = rod_to
rod_temp = from
rod_to = temp
step = 1
continue
}
step++
}
}
以上程式,建立了三個堆疊來儲存碟片(數值愈小的碟片尺寸愈大。0表示桿子的底部,以一個尺寸最大的碟片來模擬,所以移不走)。再來就是要處理每個循環的第四步,碟片要怎麼移動了。其實這個很簡單,我們只需判斷前兩小的碟片所在的另外兩個桿子,看它們頂部儲存的數值哪個比較大,就從頂部數值比較大的桿子移到頂部數值比較小的桿子。
所以最終的程式碼如下:
fn move_disk(stacks: &mut [Vec<usize>], rod_names: &[char], from: usize, to: usize) {
let disk = stacks[from].pop().unwrap();
stacks[to].push(disk);
println!("Move a disk from {} to {}.", rod_names[from], rod_names[to]);
}
pub fn hanoi_iteratively(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
let rod_names = [rod_from, rod_temp, rod_to];
let mut stacks = [Vec::new(), Vec::new(), Vec::new()];
let mut rod_from = 0;
let mut rod_temp = 1;
let mut rod_to = 2;
if disk_count & 1 == 1 {
let temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
for stack in stacks.iter_mut() {
stack.push(0);
}
for i in 1..=disk_count {
stacks[rod_from].push(i);
}
let end = 2f64.powf(disk_count as f64) as usize - 1;
let mut step = 1;
for _ in 0..end {
match step {
1 => move_disk(&mut stacks, &rod_names, rod_from, rod_temp),
2 => move_disk(&mut stacks, &rod_names, rod_from, rod_to),
3 => move_disk(&mut stacks, &rod_names, rod_temp, rod_to),
_ => {
if stacks[rod_from].last().unwrap() > stacks[rod_temp].last().unwrap() {
move_disk(&mut stacks, &rod_names, rod_from, rod_temp);
} else {
move_disk(&mut stacks, &rod_names, rod_temp, rod_from);
}
let from = rod_from;
let temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
}
step += 1;
}
}
static void moveDisk(final Stack<Integer>[] stacks, final char[] rod_names, final int from, final int to) {
final Integer disk = stacks[from].pop();
stacks[to].push(disk);
System.out.printf("Move a disk from %c to %c.%n", rod_names[from], rod_names[to]);
}
public static void hanoiIteratively(final int disk_count, char rod_from_name, char rod_temp_name, char rod_to_name) {
final char[] rod_names = new char[]{rod_from_name, rod_temp_name, rod_to_name};
final Stack<Integer>[] stacks = new Stack[]{new Stack<>(), new Stack<>(), new Stack<>()};
int rod_from = 0;
int rod_temp = 1;
int rod_to = 2;
if ((disk_count & 1) == 1) {
final int temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
for (int i = 0; i < stacks.length; ++i) {
stacks[i].push(0);
}
for (int i = 1; i <= disk_count; ++i) {
stacks[rod_from].push(i);
}
final int end = (int) Math.pow(2, disk_count) - 1;
int step = 1;
for (int i = 0; i < end; ++i) {
switch (step) {
case 1:
moveDisk(stacks, rod_names, rod_from, rod_temp);
break;
case 2:
moveDisk(stacks, rod_names, rod_from, rod_to);
break;
case 3:
moveDisk(stacks, rod_names, rod_temp, rod_to);
break;
case 4:
if (stacks[rod_from].peek() > stacks[rod_temp].peek()) {
moveDisk(stacks, rod_names, rod_from, rod_temp);
} else {
moveDisk(stacks, rod_names, rod_temp, rod_from);
}
final int from = rod_from;
final int temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
++step;
}
}
function moveDisk(stacks: number[][], rodNames: string[], from: number, to: number) {
// eslint-disable-next-line @typescript-eslint/no-non-null-assertion
const disk = stacks[from].pop()!;
stacks[to].push(disk);
console.log(`Move a disk from ${rodNames[from]} to ${rodNames[to]}.`);
}
function hanoiIteratively(diskCount: number, rodFromName: string, rodTempName: string, rodToName: string) {
const rodNames = [rodFromName, rodTempName, rodToName];
const stacks: number[][] = [[], [], []];
let rodFrom = 0;
let rodTemp = 1;
let rodTo = 2;
if ((diskCount & 1) === 1) {
const temp = rodTemp;
rodTemp = rodTo;
rodTo = temp;
}
for (const stack of stacks) {
stack.push(0);
}
for (let i = 1;i <= diskCount;i++) {
stacks[rodFrom].push(i);
}
const end = (2 ** diskCount) - 1;
let step = 1;
for (let i = 0;i < end;i++) {
switch (step) {
case 1:
moveDisk(stacks, rodNames, rodFrom, rodTemp);
break;
case 2:
moveDisk(stacks, rodNames, rodFrom, rodTo);
break;
case 3:
moveDisk(stacks, rodNames, rodTemp, rodTo);
break;
case 4: {
if (stacks[rodFrom][stacks[rodFrom].length - 1] > stacks[rodTemp][stacks[rodTemp].length - 1]) {
moveDisk(stacks, rodNames, rodFrom, rodTemp);
} else {
moveDisk(stacks, rodNames, rodTemp, rodFrom);
}
const from = rodFrom;
const temp = rodTemp;
rodFrom = rodTo;
rodTemp = from;
rodTo = temp;
step = 1;
continue;
}
}
step += 1;
}
}
type stack []int
func (s stack) Push(v int) stack {
return append(s, v)
}
func (s stack) Pop() (stack, int) {
l := len(s)
return s[:l-1], s[l-1]
}
func (s stack) Peek() int {
l := len(s)
return s[l-1]
}
func moveDisk(stacks []stack, rod_names []rune, from int, to int) {
var disk int
stacks[from], disk = stacks[from].Pop()
stacks[to] = stacks[to].Push(disk)
fmt.Printf("Move a disk from %c to %c.\n", rod_names[from], rod_names[to])
}
func hanoiIteratively(disk_count int, rod_from_name rune, rod_temp_name rune, rod_to_name rune) {
rod_names := []rune{rod_from_name, rod_temp_name, rod_to_name}
stacks := []stack{make(stack, 0), make(stack, 0), make(stack, 0)}
rod_from := 0
rod_temp := 1
rod_to := 2
if disk_count&1 == 1 {
temp := rod_temp
rod_temp = rod_to
rod_to = temp
}
for i := 0; i < len(stacks); i++ {
stacks[i] = stacks[i].Push(0)
}
for i := 1; i <= disk_count; i++ {
stacks[rod_from] = stacks[rod_from].Push(i)
}
end := int(math.Pow(2.0, float64(disk_count))) - 1
step := 1
for i := 0; i < end; i++ {
switch step {
case 1:
moveDisk(stacks, rod_names, rod_from, rod_temp)
case 2:
moveDisk(stacks, rod_names, rod_from, rod_to)
case 3:
moveDisk(stacks, rod_names, rod_temp, rod_to)
case 4:
if stacks[rod_from].Peek() > stacks[rod_temp].Peek() {
moveDisk(stacks, rod_names, rod_from, rod_temp)
} else {
moveDisk(stacks, rod_names, rod_temp, rod_from)
}
from := rod_from
temp := rod_temp
rod_from = rod_to
rod_temp = from
rod_to = temp
step = 1
continue
}
step++
}
}
這邊再介紹另一個河內塔迭代版的演算法,現實中在玩河內塔的時候也可以使用,但是會比較燒腦一點。
如果仔細觀察河內塔最短路徑的解,可以發現一個「三步一循環」的規律,而且有區分偶數和奇數的碟片數量。偶數就是「AB→AC→BC」,奇數就是「AC→AB→BC」。
什麼意思?
如果碟片數量為偶數,在這三步組成的循環中,第一步我們只需要去看A、B這兩個桿子,看是要把碟片從A桿移到B桿,還是要反過來從B桿移到A桿;第二步只需要去看A、C這兩個桿子,看是要把碟片從A桿移到C桿,還是要反過來從C桿移到A桿;第三步只需要去看B、C這兩個桿子,看是要把碟片從B桿移到C桿,還是要反過來從C桿移到B桿。
與先前同樣地,若要以程式來實作,當碟片數量為奇數時,可以先去交換B、C兩個桿子,這樣一來「三步一循環」的規律就只剩下「AB→AC→BC」了。所以可以寫出以下迭代版本的河內塔函數:
fn move_disk(stacks: &mut [Vec<usize>], rod_names: &[char], from: usize, to: usize) {
let disk = stacks[from].pop().unwrap();
stacks[to].push(disk);
println!("Move a disk from {} to {}.", rod_names[from], rod_names[to]);
}
fn move_between_rods(stacks: &mut [Vec<usize>], rod_names: &[char], x: usize, y: usize) {
if stacks[x].last().unwrap() > stacks[y].last().unwrap() {
move_disk(stacks, rod_names, x, y);
} else {
move_disk(stacks, rod_names, y, x);
}
}
pub fn hanoi_iteratively(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
let rod_names = [rod_from, rod_temp, rod_to];
let mut stacks = [Vec::new(), Vec::new(), Vec::new()];
let a = 0;
let mut b = 1;
let mut c = 2;
if disk_count & 1 == 1 {
let temp = b;
b = c;
c = temp;
}
for stack in stacks.iter_mut() {
stack.push(0);
}
for i in 1..=disk_count {
stacks[a].push(i);
}
let end = 2f64.powf(disk_count as f64) as usize - 1;
let mut step = 1;
for _ in 0..end {
match step {
1 => move_between_rods(&mut stacks, &rod_names, a, b),
2 => move_between_rods(&mut stacks, &rod_names, a, c),
_ => {
move_between_rods(&mut stacks, &rod_names, b, c);
step = 1;
continue;
}
}
step += 1;
}
}
static void moveDisk(final Stack<Integer>[] stacks, final char[] rod_names, final int from, final int to) {
final Integer disk = stacks[from].pop();
stacks[to].push(disk);
System.out.printf("Move a disk from %c to %c.%n", rod_names[from], rod_names[to]);
}
static void moveBetweenRods(final Stack<Integer>[] stacks, final char[] rod_names, final int x, final int y) {
if (stacks[x].peek() > stacks[y].peek()) {
moveDisk(stacks, rod_names, x, y);
} else {
moveDisk(stacks, rod_names, y, x);
}
}
public static void hanoiIteratively(final int disk_count, char rod_from_name, char rod_temp_name, char rod_to_name) {
final char[] rod_names = new char[]{rod_from_name, rod_temp_name, rod_to_name};
final Stack<Integer>[] stacks = new Stack[]{new Stack<>(), new Stack<>(), new Stack<>()};
final int a = 0;
int b = 1;
int c = 2;
if ((disk_count & 1) == 1) {
final int temp = b;
b = c;
c = temp;
}
for (int i = 0; i < stacks.length; ++i) {
stacks[i].push(0);
}
for (int i = 1; i <= disk_count; ++i) {
stacks[a].push(i);
}
final int end = (int) Math.pow(2, disk_count) - 1;
int step = 1;
for (int i = 0; i < end; ++i) {
switch (step) {
case 1:
moveBetweenRods(stacks, rod_names, a, b);
break;
case 2:
moveBetweenRods(stacks, rod_names, a, c);
break;
default:
moveBetweenRods(stacks, rod_names, b, c);
step = 1;
continue;
}
++step;
}
}
function moveDisk(stacks: number[][], rodNames: string[], from: number, to: number) {
const disk = stacks[from].pop();
stacks[to].push(disk);
console.log(`Move a disk from ${rodNames[from]} to ${rodNames[to]}.`);
}
function moveBetweenRods(stacks: number[][], rodNames: string[], x: number, y: number) {
if (stacks[x][stacks[x].length - 1] > stacks[y][stacks[y].length - 1]) {
moveDisk(stacks, rodNames, x, y);
} else {
moveDisk(stacks, rodNames, y, x);
}
}
function hanoiIteratively(diskCount: number, rodFromName: string, rodTempName: string, rodToName: string) {
const rodNames = [rodFromName, rodTempName, rodToName];
const stacks: number[][] = [[], [], []];
const a = 0;
let b = 1;
let c = 2;
if ((diskCount & 1) === 1) {
const temp = b;
b = c;
c = temp;
}
for (const stack of stacks) {
stack.push(0);
}
for (let i = 1;i <= diskCount;i++) {
stacks[a].push(i);
}
const end = (2 ** diskCount) - 1;
let step = 1;
for (let i = 0;i < end;i++) {
switch (step) {
case 1:
moveBetweenRods(stacks, rodNames, a, b);
break;
case 2:
moveBetweenRods(stacks, rodNames, a, c);
break;
case 3:
moveBetweenRods(stacks, rodNames, b, c);
step = 1;
continue;
}
step += 1;
}
}
type stack []int
func (s stack) Push(v int) stack {
return append(s, v)
}
func (s stack) Pop() (stack, int) {
l := len(s)
return s[:l-1], s[l-1]
}
func (s stack) Peek() int {
l := len(s)
return s[l-1]
}
func moveDisk(stacks []stack, rod_names []rune, from int, to int) {
var disk int
stacks[from], disk = stacks[from].Pop()
stacks[to] = stacks[to].Push(disk)
fmt.Printf("Move a disk from %c to %c.\n", rod_names[from], rod_names[to])
}
func moveBetweenRods(stacks []stack, rod_names []rune, x int, y int) {
if stacks[x].Peek() > stacks[y].Peek() {
moveDisk(stacks, rod_names, x, y)
} else {
moveDisk(stacks, rod_names, y, x)
}
}
func hanoiIteratively(disk_count int, rod_from_name rune, rod_temp_name rune, rod_to_name rune) {
rod_names := []rune{rod_from_name, rod_temp_name, rod_to_name}
stacks := []stack{make(stack, 0), make(stack, 0), make(stack, 0)}
a := 0
b := 1
c := 2
if disk_count&1 == 1 {
temp := b
b = c
c = temp
}
for i := 0; i < len(stacks); i++ {
stacks[i] = stacks[i].Push(0)
}
for i := 1; i <= disk_count; i++ {
stacks[a] = stacks[a].Push(i)
}
end := int(math.Pow(2.0, float64(disk_count))) - 1
step := 1
for i := 0; i < end; i++ {
switch step {
case 1:
moveBetweenRods(stacks, rod_names, a, b)
case 2:
moveBetweenRods(stacks, rod_names, a, c)
case 3:
moveBetweenRods(stacks, rod_names, b, c)
step = 1
continue
}
step++
}
}
不用堆疊空間的河內塔迭代演算法
回顧我們一開始介紹的遞迴版本的河內塔演算法:
步驟一:移動A桿子上的#{{n - 1}}#個碟片到B桿子上。
步驟二:移動A桿子剩下的一個碟片到C桿子上。
步驟三:移動B桿子上的所有(#{{n - 1}}#個)碟片到C桿子上。
其實要把已知步驟的#{{n}}#個碟片從一個桿子搬到另一個桿子上是很容易的。舉例來說,若要把三個碟片從A桿搬到C桿,搬移步驟如下:
Move a disk from A to B.
Move a disk from C to B.
Move a disk from A to C.
Move a disk from B to A.
Move a disk from B to C.
Move a disk from A to C.
而若要把三個碟片從A桿搬到B桿,搬移步驟如下:
Move a disk from A to C.
Move a disk from B to C.
Move a disk from A to B.
Move a disk from C to A.
Move a disk from C to B.
Move a disk from A to B.
有沒有發現?其實我們只要把從A桿搬到C桿的路線中的B、C桿子交換就可以了。
而若要把三個碟片從B桿搬到C桿,搬移步驟如下:
Move a disk from B to A.
Move a disk from C to A.
Move a disk from B to C.
Move a disk from A to B.
Move a disk from A to C.
Move a disk from B to C.
有沒有發現?其實我們只要把從A桿搬到B桿的路線中的A換成B、B換成C、C換成A。
所以呢?
根據這個發現,要把#{{n}}#個碟片從A桿搬到C桿,我們可以先將#{{n - 1}}#個碟片搬到C桿(可沿用計算#{{n - 1}}#個碟片時找出的解),接著再把B、C桿子交換(利用A桿到C桿的路線,把B、C桿子交換),然後再把剩下的一個碟片從A桿搬到C桿,最後再把B桿的#{{n - 1}}#個碟片搬到C桿(利用A桿到B桿的路線,把A換成B、B換成C、C換成A)。
為了快速地將路線進行置換,我們可以把六種(#{{P^3_2 = 6}}#)移動方式編號如下,稱作「路線表」好了。
- 0: A→B
- 1: A→C
- 2: B→A
- 3: B→C
- 4: C→A
- 5: C→B
把「路線表」的B、C桿子交換,並依照原來A→B、A→C、B→A、……的方式來排序,結果如下:
- 1: A→B
- 0: A→C
- 4: B→A
- 5: B→C
- 2: C→A
- 3: C→B
這樣做可以讓我們利用原先路線的編號,快速地對應到把B、C桿子交換後的結果。
把「路線表」的A換成C、C換成B、B換成A,並依照原來A→B、A→C、B→A、……的方式來排序,結果如下:
- 3: A→B
- 2: A→C
- 5: B→A
- 4: B→C
- 0: C→A
- 1: C→B
這樣做可以讓我們利用原先路線的編號,快速地對應到把A換成B、B換成C、C換成A後的結果。
再來我們就可以實作出不需堆疊空間(但需要暫存結果)的河內塔迭代函數:
pub fn hanoi(disk_count: usize, a: char, b: char, c: char) {
let bc_swap = [1, 0, 4, 5, 2, 3];
let a2b_b2c_c2a = [3, 2, 5, 4, 0, 1];
let number_of_total_steps = 2f64.powf(disk_count as f64) as usize - 1;
let mut route = Vec::with_capacity(number_of_total_steps);
unsafe {
route.set_len(number_of_total_steps);
}
let mut size = 1;
route[0] = 1;
for _ in 2..=disk_count {
for e in route.iter_mut().take(size) {
*e = bc_swap[*e];
}
route[size] = 1;
for i in 0..size {
route[size + i + 1] = a2b_b2c_c2a[route[i]];
}
size <<= 1;
size += 1;
}
for s in route {
let (rod_from, rod_to) = match s {
0 => (a, b),
1 => (a, c),
2 => (b, a),
3 => (b, c),
4 => (c, a),
_ => (c, b),
};
println!("Move a disk from {rod_from} to {rod_to}.");
}
}
public static void hanoi(final int disk_count, final char a, final char b, final char c) {
final int[] bc_swap = new int[]{1, 0, 4, 5, 2, 3};
final int[] a2b_b2c_c2a = new int[]{3, 2, 5, 4, 0, 1};
final int number_of_total_steps = (int) Math.pow(2, disk_count) - 1;
final int[] route = new int[number_of_total_steps];
int size = 1;
route[0] = 1;
for (int i = 2; i <= disk_count; ++i) {
for (int j = 0; j < size; ++j) {
route[j] = bc_swap[route[j]];
}
route[size] = 1;
for (int j = 0; j < size; ++j) {
route[size + j + 1] = a2b_b2c_c2a[route[j]];
}
size <<= 1;
size += 1;
}
for (final int s : route) {
final char rod_from, rod_to;
switch (s) {
case 0:
rod_from = a;
rod_to = b;
break;
case 1:
rod_from = a;
rod_to = c;
break;
case 2:
rod_from = b;
rod_to = a;
break;
case 3:
rod_from = b;
rod_to = c;
break;
case 4:
rod_from = c;
rod_to = a;
break;
default:
rod_from = c;
rod_to = b;
}
System.out.printf("Move a disk from %c to %c.%n", rod_from, rod_to);
}
}
function hanoi(diskCount: number, a: string, b: string, c: string) {
const bcSwap = [
1, 0, 4, 5, 2, 3,
];
const a2bB2cC2a = [
3, 2, 5, 4, 0, 1,
];
const numberOfTotalSteps = (2 ** diskCount) - 1;
const route = new Array<number>(numberOfTotalSteps);
let size = 1;
route[0] = 1;
for (let i = 2;i <= diskCount;i++) {
for (let j = 0;j < size;j++) {
route[j] = bcSwap[route[j]];
}
route[size] = 1;
for (let j = 0;j < size;j++) {
route[size + j + 1] = a2bB2cC2a[route[j]];
}
size <<= 1;
size += 1;
}
for (const r of route) {
let rodFrom;
let rodTo;
switch (r) {
case 0:
rodFrom = a;
rodTo = b;
break;
case 1:
rodFrom = a;
rodTo = c;
break;
case 2:
rodFrom = b;
rodTo = a;
break;
case 3:
rodFrom = b;
rodTo = c;
break;
case 4:
rodFrom = c;
rodTo = a;
break;
default:
rodFrom = c;
rodTo = b;
}
console.log(`Move a disk from ${rodFrom} to ${rodTo}.`);
}
}
func hanoi(disk_count int, a rune, b rune, c rune) {
bc_swap := [...]int{1, 0, 4, 5, 2, 3}
a2b_b2c_c2a := [...]int{3, 2, 5, 4, 0, 1}
number_of_total_steps := int(math.Pow(2.0, float64(disk_count))) - 1
route := make([]int, number_of_total_steps)
size := 1
route[0] = 1
for i := 2; i <= disk_count; i++ {
for j := 0; j < size; j++ {
route[j] = bc_swap[route[j]]
}
route[size] = 1
for j := 0; j < size; j++ {
route[size+j+1] = a2b_b2c_c2a[route[j]]
}
size <<= 1
size += 1
}
for _, s := range route {
var rod_from, rod_to rune
switch s {
case 0:
rod_from = a
rod_to = b
case 1:
rod_from = a
rod_to = c
case 2:
rod_from = b
rod_to = a
case 3:
rod_from = b
rod_to = c
case 4:
rod_from = c
rod_to = a
default:
rod_from = c
rod_to = b
}
fmt.Printf("Move a disk from %c to %c.\n", rod_from, rod_to)
}
}
讓程式能輸出碟片編號
為了讓各位更容易了解,上面提供的程式碼都沒有輸出究竟是哪個碟片被移動了。所以最後就來提供一下,這些程式碼的「完整版」吧!
首先是遞迴版本的河內塔。(碟片數字愈小,尺寸愈小)
pub fn hanoi(disk_count: usize, rod_from: char, rod_temp: char, rod_to: char) {
if disk_count >= 1 {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
println!("Move #{disk_count} from {rod_from} to {rod_to}.");
hanoi(disk_count - 1, rod_temp, rod_from, rod_to);
}
}
public static void hanoi(final int disk_count, final char rod_from, final char rod_temp, final char rod_to) {
if (disk_count >= 1) {
hanoi(disk_count - 1, rod_from, rod_to, rod_temp);
System.out.printf("Move #%d from %c to %c.%n", disk_count, rod_from, rod_to);
hanoi(disk_count - 1, rod_temp, rod_from, rod_to);
}
}
function hanoi(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
if (diskCount >= 1) {
hanoi(diskCount - 1, rodFrom, rodTo, rodTemp);
console.log(`Move #${diskCount} from ${rodFrom} to ${rodTo}.`);
hanoi(diskCount - 1, rodTemp, rodFrom, rodTo);
}
}
func hanoi(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
if disk_count >= 1 {
hanoi(disk_count-1, rod_from, rod_to, rod_temp)
fmt.Printf("Move #%d from %c to %c.\n", disk_count, rod_from, rod_to)
hanoi(disk_count-1, rod_temp, rod_from, rod_to)
}
}
再來是「四步一循環」與「三步一循環」的堆疊空間迭代版所用的move_disk或moveDisk函數。(碟片數字愈小,尺寸愈大)
fn move_disk(stacks: &mut [Vec<usize>], rod_names: &[char], from: usize, to: usize) {
let disk = stacks[from].pop().unwrap();
stacks[to].push(disk);
println!("Move #{} from {} to {}.", disk, rod_names[from], rod_names[to]);
}
static void moveDisk(final Stack<Integer>[] stacks, final char[] rod_names, final int from, final int to) {
final Integer disk = stacks[from].pop();
stacks[to].push(disk);
System.out.printf("Move #%d from %c to %c.%n", disk, rod_names[from], rod_names[to]);
}
function moveDisk(stacks: number[][], rodNames: string[], from: number, to: number) {
// eslint-disable-next-line @typescript-eslint/no-non-null-assertion
const disk = stacks[from].pop()!;
stacks[to].push(disk);
console.log(`Move #${disk} from ${rodNames[from]} to ${rodNames[to]}.`);
}
func moveDisk(stacks []stack, rod_names []rune, from int, to int) {
var disk int
stacks[from], disk = stacks[from].Pop()
stacks[to] = stacks[to].Push(disk)
fmt.Printf("Move #%d from %c to %c.\n", disk, rod_names[from], rod_names[to])
}
最後是無堆疊空間的迭代版河內塔。(碟片數字愈小,尺寸愈小)
pub fn hanoi(disk_count: usize, a: char, b: char, c: char) {
let bc_swap = [1, 0, 4, 5, 2, 3];
let a2b_b2c_c2a = [3, 2, 5, 4, 0, 1];
let number_of_total_steps = 2f64.powf(disk_count as f64) as usize - 1;
let mut route = Vec::with_capacity(number_of_total_steps);
let mut disks = Vec::with_capacity(number_of_total_steps);
unsafe {
route.set_len(number_of_total_steps);
disks.set_len(number_of_total_steps);
}
let mut size = 1;
route[0] = 1;
disks[0] = 1;
for n in 2..=disk_count {
for e in route.iter_mut().take(size) {
*e = bc_swap[*e];
}
route[size] = 1;
disks[size] = n;
for i in 0..size {
route[size + i + 1] = a2b_b2c_c2a[route[i]];
}
unsafe {
copy_nonoverlapping(disks.as_ptr(), disks[size + 1..].as_mut_ptr(), size);
}
size <<= 1;
size += 1;
}
for (i, s) in route.into_iter().enumerate() {
let (rod_from, rod_to) = match s {
0 => (a, b),
1 => (a, c),
2 => (b, a),
3 => (b, c),
4 => (c, a),
_ => (c, b),
};
println!("Move #{} from {} to {}.", disks[i], rod_from, rod_to);
}
}
public static void hanoi(final int disk_count, final char a, final char b, final char c) {
final int[] bc_swap = new int[]{1, 0, 4, 5, 2, 3};
final int[] a2b_b2c_c2a = new int[]{3, 2, 5, 4, 0, 1};
final int number_of_total_steps = (int) Math.pow(2, disk_count) - 1;
final int[] route = new int[number_of_total_steps];
final int[] disks = new int[number_of_total_steps];
int size = 1;
route[0] = 1;
disks[0] = 1;
for (int i = 2; i <= disk_count; ++i) {
for (int j = 0; j < size; ++j) {
route[j] = bc_swap[route[j]];
}
route[size] = 1;
disks[size] = i;
for (int j = 0; j < size; ++j) {
route[size + j + 1] = a2b_b2c_c2a[route[j]];
}
System.arraycopy(disks, 0, disks, size + 1, size);
size <<= 1;
size += 1;
}
for (int i = 0; i < number_of_total_steps; ++i) {
final int s = route[i];
final char rod_from, rod_to;
switch (s) {
case 0:
rod_from = a;
rod_to = b;
break;
case 1:
rod_from = a;
rod_to = c;
break;
case 2:
rod_from = b;
rod_to = a;
break;
case 3:
rod_from = b;
rod_to = c;
break;
case 4:
rod_from = c;
rod_to = a;
break;
default:
rod_from = c;
rod_to = b;
}
System.out.printf("Move #%d from %c to %c.%n", disks[i], rod_from, rod_to);
}
}
function hanoi(diskCount: number, a: string, b: string, c: string) {
const bcSwap = [
1, 0, 4, 5, 2, 3,
];
const a2bB2cC2a = [
3, 2, 5, 4, 0, 1,
];
const numberOfTotalSteps = (2 ** diskCount) - 1;
const route = new Array<number>(numberOfTotalSteps);
const disks = new Array<number>(numberOfTotalSteps);
let size = 1;
route[0] = 1;
disks[0] = 1;
for (let i = 2;i <= diskCount;i++) {
for (let j = 0;j < size;j++) {
route[j] = bcSwap[route[j]];
}
route[size] = 1;
disks[size] = i;
for (let j = 0;j < size;j++) {
const index = size + j + 1;
route[index] = a2bB2cC2a[route[j]];
disks[index] = disks[j];
}
size <<= 1;
size += 1;
}
for (let i = 0;i < numberOfTotalSteps;i++) {
const r = route[i];
let rodFrom;
let rodTo;
switch (r) {
case 0:
rodFrom = a;
rodTo = b;
break;
case 1:
rodFrom = a;
rodTo = c;
break;
case 2:
rodFrom = b;
rodTo = a;
break;
case 3:
rodFrom = b;
rodTo = c;
break;
case 4:
rodFrom = c;
rodTo = a;
break;
default:
rodFrom = c;
rodTo = b;
}
console.log(`Move #${disks[i]} from ${rodFrom} to ${rodTo}.`);
}
}
func hanoi(disk_count int, a rune, b rune, c rune) {
bc_swap := [...]int{1, 0, 4, 5, 2, 3}
a2b_b2c_c2a := [...]int{3, 2, 5, 4, 0, 1}
number_of_total_steps := int(math.Pow(2.0, float64(disk_count))) - 1
route := make([]int, number_of_total_steps)
disks := make([]int, number_of_total_steps)
size := 1
route[0] = 1
disks[0] = 1
for i := 2; i <= disk_count; i++ {
for j := 0; j < size; j++ {
route[j] = bc_swap[route[j]]
}
route[size] = 1
disks[size] = i
for j := 0; j < size; j++ {
route[size+j+1] = a2b_b2c_c2a[route[j]]
}
copy(disks[size+1:], disks[:size])
size <<= 1
size += 1
}
for i, s := range route {
var rod_from, rod_to rune
switch s {
case 0:
rod_from = a
rod_to = b
case 1:
rod_from = a
rod_to = c
case 2:
rod_from = b
rod_to = a
case 3:
rod_from = b
rod_to = c
case 4:
rod_from = c
rod_to = a
default:
rod_from = c
rod_to = b
}
fmt.Printf("Move #%d from %c to %c.\n", disks[i], rod_from, rod_to)
}
}
利用碟片的輸出規律來實現不用堆疊空間的河內塔迭代版函數
在實作出有輸出碟片編號的河內塔程式後,可以試玩一下,會發現輸出的碟片編號其實也有規律。
如果我們只讓河內塔程式輸出碟片編號,四個碟片的結果如下:
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
五個碟片的結果如下:
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
六個碟片的結果如下:
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 6 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
看出來了嗎?這擺明就是一個數列嘛!而且可以找出以下公式來直接求得指定項數的值。
#{{{
a_n = \lfloor log_2{(n \text{ } XOR \text{ } (n + 1))} \rfloor + 1, n \in \mathbb{N^0}
}}}#
也就是說,我們先前利用「四步一循環」和「三步一循環」規律來實作的迭代版的河內塔函數,可以改成無堆疊空間的版本,只需要額外記錄當下的所有碟片在哪個桿子上即可,而且也可以順便將它們修改成以「碟片數字愈小,尺寸愈小」的方式來輸出。
將「四步一循環」修改後的程式碼如下:
fn move_disk(disk_positions: &mut [char], disk: usize, to: char) {
println!("Move #{} from {} to {}.", disk + 1, disk_positions[disk], to);
disk_positions[disk] = to;
}
pub fn hanoi_iteratively(disk_count: usize, mut rod_from: char, mut rod_temp: char, mut rod_to: char) {
let mut disk_positions = vec![rod_from; disk_count];
if disk_count & 1 == 1 {
let temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
let end = 2f64.powf(disk_count as f64) as usize - 1;
let mut step = 1;
for i in 0..end {
let disk = ((i ^ (i + 1)) as f64).log2().floor() as usize;
match step {
1 => move_disk(&mut disk_positions, disk, rod_temp),
2 | 3 => move_disk(&mut disk_positions, disk, rod_to),
_ => {
if disk_positions[disk] == rod_from {
move_disk(&mut disk_positions, disk, rod_temp)
} else {
move_disk(&mut disk_positions, disk, rod_from)
}
let from = rod_from;
let temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
}
step += 1;
}
}
static void moveDisk(final char[] disk_positions, final int disk, final char to) {
System.out.printf("Move #%d from %c to %c.%n", disk + 1, disk_positions[disk], to);
disk_positions[disk] = to;
}
public static void hanoiIteratively(final int disk_count, char rod_from, char rod_temp, char rod_to) {
final char[] disk_positions = new char[disk_count];
Arrays.fill(disk_positions, rod_from);
if ((disk_count & 1) == 1) {
final char temp = rod_temp;
rod_temp = rod_to;
rod_to = temp;
}
final int end = (int) Math.pow(2, disk_count) - 1;
int step = 1;
for (int i = 0; i < end; ++i) {
final int disk = (int) Math.floor(Math.log(i ^ (i + 1)) / Math.log(2));
switch (step) {
case 1:
moveDisk(disk_positions, disk, rod_temp);
break;
case 2:
case 3:
moveDisk(disk_positions, disk, rod_to);
break;
case 4:
if (disk_positions[disk] == rod_from) {
moveDisk(disk_positions, disk, rod_temp);
} else {
moveDisk(disk_positions, disk, rod_from);
}
final char from = rod_from;
final char temp = rod_temp;
rod_from = rod_to;
rod_temp = from;
rod_to = temp;
step = 1;
continue;
}
++step;
}
}
function moveDisk(diskPositions: string[], disk: number, to: string) {
console.log(`Move #${disk + 1} from ${diskPositions[disk]} to ${to}.`);
diskPositions[disk] = to;
}
function hanoiIteratively(diskCount: number, rodFrom: string, rodTemp: string, rodTo: string) {
const diskPositions = new Array<string>(diskCount).fill(rodFrom);
if ((diskCount & 1) === 1) {
const temp = rodTemp;
rodTemp = rodTo;
rodTo = temp;
}
const end = (2 ** diskCount) - 1;
let step = 1;
for (let i = 0;i < end;i++) {
const disk = Math.floor(Math.log2(i ^ (i + 1)));
switch (step) {
case 1:
moveDisk(diskPositions, disk, rodTemp);
break;
case 2:
case 3:
moveDisk(diskPositions, disk, rodTo);
break;
case 4: {
if (diskPositions[disk] === rodFrom) {
moveDisk(diskPositions, disk, rodTemp);
} else {
moveDisk(diskPositions, disk, rodTemp);
}
const from = rodFrom;
const temp = rodTemp;
rodFrom = rodTo;
rodTemp = from;
rodTo = temp;
step = 1;
continue;
}
}
step += 1;
}
}
func moveDisk(disk_positions []rune, disk int, to rune) {
fmt.Printf("Move #%d from %c to %c.\n", disk+1, disk_positions[disk], to)
disk_positions[disk] = to
}
func hanoiIteratively(disk_count int, rod_from rune, rod_temp rune, rod_to rune) {
disk_positions := make([]rune, disk_count)
for i := 0; i < disk_count; i++ {
disk_positions[i] = rod_from
}
if disk_count&1 == 1 {
temp := rod_temp
rod_temp = rod_to
rod_to = temp
}
end := int(math.Pow(2.0, float64(disk_count))) - 1
step := 1
for i := 0; i < end; i++ {
disk := int(math.Floor(math.Log2(float64(i ^ (i + 1)))))
switch step {
case 1:
moveDisk(disk_positions, disk, rod_temp)
case 2, 3:
moveDisk(disk_positions, disk, rod_to)
case 4:
if disk_positions[disk] == rod_from {
moveDisk(disk_positions, disk, rod_temp)
} else {
moveDisk(disk_positions, disk, rod_from)
}
from := rod_from
temp := rod_temp
rod_from = rod_to
rod_temp = from
rod_to = temp
step = 1
continue
}
step++
}
}
將「三步一循環」修改後的程式碼如下:
fn move_disk(disk_positions: &mut [char], disk: usize, to: char) {
println!("Move #{} from {} to {}.", disk + 1, disk_positions[disk], to);
disk_positions[disk] = to;
}
fn move_between_rods(disk_positions: &mut [char], disk: usize, x: char, y: char) {
if disk_positions[disk] == x {
move_disk(disk_positions, disk, y);
} else {
move_disk(disk_positions, disk, x);
}
}
pub fn hanoi_iteratively(disk_count: usize, a: char, mut b: char, mut c: char) {
let mut disk_positions = vec![a; disk_count];
if disk_count & 1 == 1 {
let temp = b;
b = c;
c = temp;
}
let end = 2f64.powf(disk_count as f64) as usize - 1;
let mut step = 1;
for i in 0..end {
let disk = ((i ^ (i + 1)) as f64).log2().floor() as usize;
match step {
1 => move_between_rods(&mut disk_positions, disk, a, b),
2 => move_between_rods(&mut disk_positions, disk, a, c),
_ => {
move_between_rods(&mut disk_positions, disk, b, c);
step = 1;
continue;
}
}
step += 1;
}
}
static void moveDisk(final char[] disk_positions, final int disk, final char to) {
System.out.printf("Move #%d from %c to %c.%n", disk + 1, disk_positions[disk], to);
disk_positions[disk] = to;
}
static void moveBetweenRods(final char[] disk_positions, final int disk, final char x, final char y) {
if (disk_positions[disk] == x) {
moveDisk(disk_positions, disk, y);
} else {
moveDisk(disk_positions, disk, x);
}
}
public static void hanoiIteratively(final int disk_count, final char a, char b, char c) {
final char[] disk_positions = new char[disk_count];
Arrays.fill(disk_positions, a);
if ((disk_count & 1) == 1) {
final char temp = b;
b = c;
c = temp;
}
final int end = (int) Math.pow(2, disk_count) - 1;
int step = 1;
for (int i = 0; i < end; ++i) {
final int disk = (int) Math.floor(Math.log(i ^ (i + 1)) / Math.log(2));
switch (step) {
case 1:
moveBetweenRods(disk_positions, disk, a, b);
break;
case 2:
moveBetweenRods(disk_positions, disk, a, c);
break;
default:
moveBetweenRods(disk_positions, disk, b, c);
step = 1;
continue;
}
++step;
}
}
function moveDisk(diskPositions: string[], disk: number, to: string) {
console.log(`Move #${disk + 1} from ${diskPositions[disk]} to ${to}.`);
diskPositions[disk] = to;
}
function moveBetweenRods(diskPositions: string[], disk: number, x: string, y: string) {
if (diskPositions[disk] === x) {
moveDisk(diskPositions, disk, y);
} else {
moveDisk(diskPositions, disk, x);
}
}
function hanoiIteratively(diskCount: number, a: string, b: string, c: string) {
const diskPositions = new Array<string>(diskCount).fill(a);
if ((diskCount & 1) === 1) {
const temp = b;
b = c;
c = temp;
}
const end = (2 ** diskCount) - 1;
let step = 1;
for (let i = 0;i < end;i++) {
const disk = Math.floor(Math.log2(i ^ (i + 1)));
switch (step) {
case 1:
moveBetweenRods(diskPositions, disk, a, b);
break;
case 2:
moveBetweenRods(diskPositions, disk, a, c);
break;
case 3:
moveBetweenRods(diskPositions, disk, b, c);
step = 1;
continue;
}
step += 1;
}
}
func moveDisk(disk_positions []rune, disk int, to rune) {
fmt.Printf("Move #%d from %c to %c.\n", disk+1, disk_positions[disk], to)
disk_positions[disk] = to
}
func moveBetweenRods(disk_positions []rune, disk int, x rune, y rune) {
if disk_positions[disk] == x {
moveDisk(disk_positions, disk, y)
} else {
moveDisk(disk_positions, disk, x)
}
}
func hanoiIteratively(disk_count int, a rune, b rune, c rune) {
disk_positions := make([]rune, disk_count)
for i := 0; i < disk_count; i++ {
disk_positions[i] = a
}
if disk_count&1 == 1 {
temp := b
b = c
c = temp
}
end := int(math.Pow(2.0, float64(disk_count))) - 1
step := 1
for i := 0; i < end; i++ {
disk := int(math.Floor(math.Log2(float64(i ^ (i + 1)))))
switch step {
case 1:
moveBetweenRods(disk_positions, disk, a, b)
case 2:
moveBetweenRods(disk_positions, disk, a, c)
case 3:
moveBetweenRods(disk_positions, disk, b, c)
step = 1
continue
}
step++
}
}